Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
RECUpERAR IMAGENES ESTUD11,12,13,14,15)
Estudios sobre Riges reales. Konya. Aksarai (Turquía) (perteneciente a Decoración Geométrica Islámica)
Veamos ahora una red interesante porque pertenece a la poco variada de 10, que s
|
|
|
Konya: Akasaray Medressa, Turquía. Huand külliyesi |
abemos difícil de ampliar, aunque es muy frecuente su uso. La tomamos de un libro del ministerio de cultura turco sobre este arte en su aplicación seljúcida ( (Selçuklu Çagi): Mülayim, Selçuk; Anadolu Türk Mimarisinde Geometrik Süslemeler, Kültur ve Turism Bacanligi. (no consta el año). pag.183). Este tipo de lacería en más dura que la andalusí, por ejemplo, porque contienen frecuentes ángulos agudos y triángulos. Se trata de una impresión general, no estudiada en detalle.
La figura 1 reproduce un panel que enmarca el arco de entrada en Huand Külliyesi, pero rotando el panel que la porta, para poner de manifiesto el método de su trazado, que quedaba precisamente enmascarado por su posición en ese panel: no coinciden las direcciones principales de la red de 10 con las del rectángulo que enmarca el diseño.
Red
Es la de 10, evidentemente pues hay sólo diez direcciones equidistante en ángulo, a las que todas las cintas o tiras son paralelas.
Ña secuencia de distancias consecutivas es en todos las direcciones, .....c a a a c a a a c , o sea periódica aparentemente con período (comenzado arbitrariamente por la menor, c, la calle: `[c a a a]. Pero enseguida observamos que esa secuencia se ha trasladando en cada fila (a la derecha si subimos)
O sea, subiendo fila, las dos rosas se alinean mediante su calle central, común, mientras que a la izquierda se alinean por las bisectrices. Los centros de las rosas o signos se disponen en filas algo desplazadas de centros equidistantes, formando paralelepípedos inclinados a la izquierda, 18ª (pi/10) respecto a la vertical. A la derecha, el ángulo es 36º+18º o sea 54º. Se forman así triángulos isósceles, representados en la tercera figura, cuyos ángulos suman 72º + 2 * 54º = 180º, como debe ser.


Esta solución, aunque no nos parece muy elegante desde el punto de vista geom´etrico, funciona al disimular las tiras el salto de red entre filas contiguas.
La disposición habitual es Al Andalus es más sencilla, correspondiendo a la red
La disposición es
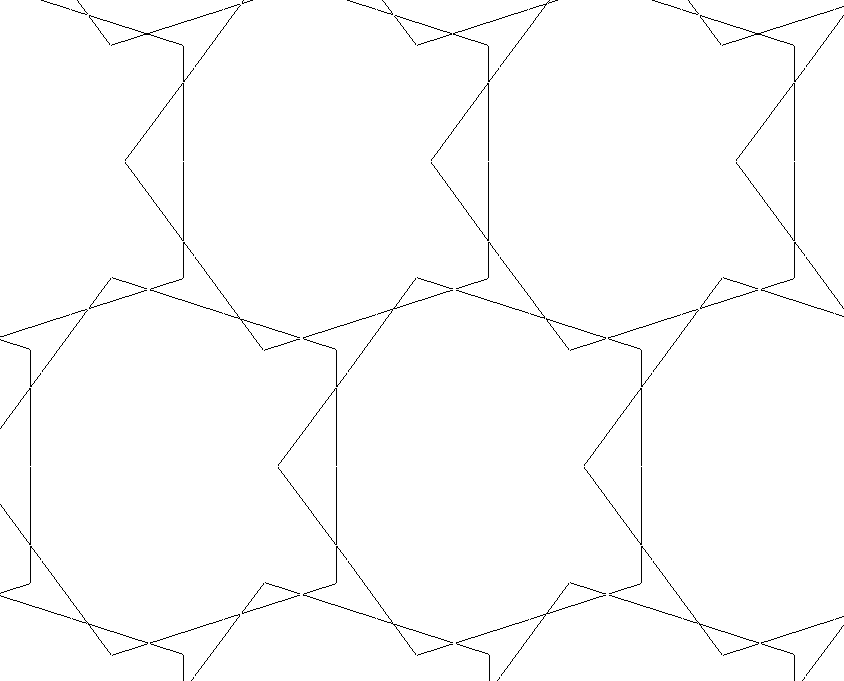
y la red
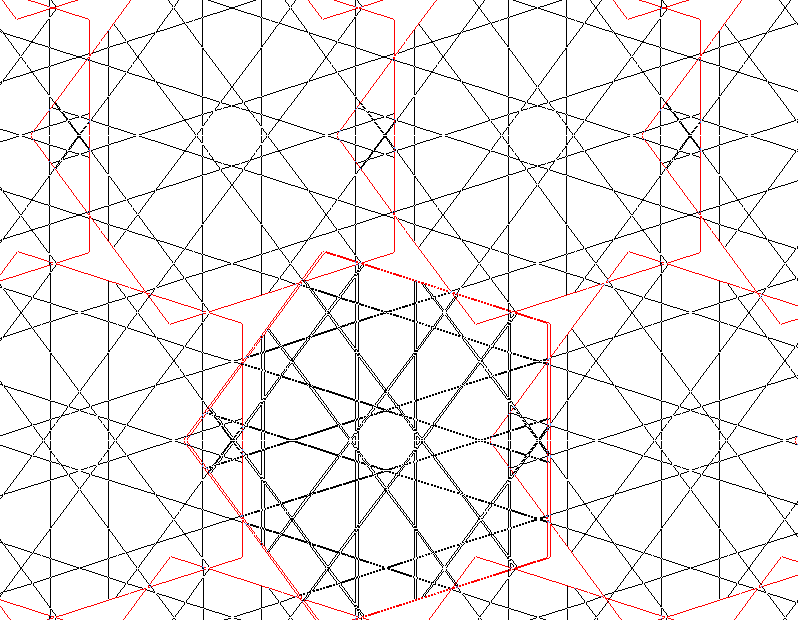
Vuelta al Principio Última
actualización:
lunes, 06 de agosto de 2018 Visitantes: