─────────────────────────────────────────────────────────────────

E D U C A C I O N M U S I C A L. T E M A A . 1 3

I N S T R U M E N T O S

─────────────────────────────────────────────────────────────────

INTRODUCCIÓN

En este tema abordamos primeramente los instrumentos musicales, se su naturaleza, y en relación con la educación musical primaria: folklore y construcción de un instrumento.

En una segunda parte se aborda la naturaleza del sonido musical, sobre todo en el aspecto tonal. En este aspecto constituye el elemento objetivo que da lugar al subjetivo, estudiado en el tema A.15. sobre Percepción.

INDICE

A.13.1. Los instrumentos musicales.

A.13.2. Producción del sonido en un instrumento musical

A.13.3. Instrumentos en la enseñanza primaria

A.13.4. Instrumentos elementales

A.13.4.1. Construcción de una flauta en el Aula.

A.13.5. Instrumentos folklóricos.

A.13.6. Producción del sonido musical en relación al Tono.

A.13.6.1.Tiempo, Vibración y Frecuencia.

A.13.6.2.Funciones Periódicas, Espectro y Descomposición de Fourier

A.13.6.3. Cuerdas y Tubos

A.13.6.5. Sonidos sin Tono.

A.13.6.3. Medida de Intervalos mediante Fracciones

A.13.7. Intervalos del Tono.

A.13.7.1. Intervalos tonales. Definición.

A.13.7.2. Medida de Intervalos mediante Fracciones

A.13.7.3. Armónicos y Espiral armónica

A.13.7.4. Intervalos Naturales

A.13.7.5. Medidas Logarítmicas de de Intervalos. El Cent.

A.13.7.6. Afinación absoluta y relativa basada en el semitono temperado.

A.13.7.7. Afinación absoluta y relativa basada en la coma Hölder.

A.13.7.8. Composición de intervalos

A.13.7.9. División y Descomposición de intervalos

A.13.8. Bibliografía.

A.13.1. Los instrumentos musicales.

───────────────────────────────

Podemos sistematizar nuestro conocimiento de la naturaleza del instrumento musical acudiendo a las siguientes características:

Un instrumento musical es un objeto que emite sonidos musicales, controlado por un ser humano. Esta sencilla definición rechaza ya muchos objetos: por ejemplo, la radio, que emite sonidos musicales pero no por acción humana (salvo la trivial de encenderlo o apagarlo). Ni una pared, aunque emita sonido al golpearla, porque no es emite sonidos musicales. No obstante el concepto de lo musical no está tan claro y definido.

La principal característica funcional de un instrumento musical es que sea controlable: es decir, que reaccione a las acciones humanas en un tiempo pequeño, para que el músico se exprese a través de él. Cuando golpeamos una campanilla, suena al momento: es controlable. Pero si su reacción es tardía, deja de serlo, su respuesta no pertenece ya al 'presente' musical.

Llamamos musical a un sonido que presenta todas o alguna de las cualidades o rasgos que la tradición ha consagrado como musicales: tono, timbre, intensidad, duración. Ahora bien como todo objeto puede ser golpeado con un cierto ritmo, en sentido amplio, todo objeto puede ser musical, o formar parte de un conjunto musical; en este caso ampliamos la definición anterior a un grupo de objetos que, en su conjunto emiten sonidos musicales controlados por un(os) ser(es) humano(s).

Hay no obstante limitaciones de orden práctico: portabilidad, controlabilidad o facilidad de manipulación, fuerza necesaria, tamaño de la mano o pie necesarios para esa manipulación, etc.

Estas definiciones, que no pretenden limitar, sino sugerir, nos ofrecen multitud e posibilidades; y por supuesto, todos los instrumentos más o menos sofisticados llamado instrumentos musicales en occidente: violín y familia, piano y familia, trompeta y familia, clarinete y familia, etc.

A.13.2. Instrumentos en la enseñanza primaria

───────────────────────────────────────────────

Los instrumentos cultos citados, excelsos en sus posibilidades, como lo prueban las obras que constituyen nuestro patrimonio musical, no son probablemente los más adecuados para la educación musical primaria de los niños, pala la iniciación a la música. En efecto, su sofisticación hace difícil su control: el instrumento emite por sí sólo por decirlo así, y el niño no obtiene una respuesta inmediata y gratificante a su acción (pensemos en cuántos años hacen falta para que el violín de un principiante dé placer musical a los que le rodean. )tres, cuatro?.

Por su parte el piano, relativamente fácil de manejar para producir un sonido, o una melodía, deviene extremadamente difícil dada la complejidad de la armonía y polifonía que el intérprete debe concebir, producir y controlar simultáneamente: es demasiado abstracto. Por otra parte, el piano como instrumento temperado, es decir, que falsea ligeramente las consonancias, no es el más adecuado para enseñarlas precisamente.

asimismo los instrumentos de viento, cuya afinación precisa necesita un preconocimiento del sonido por parte del intérprete para controlar la emisión con vistas a su obtención, no puede ser por eso mismo un maestro de esas consonancias en la iniciación musical.

Nos quedan pues instrumentos sencillos de ejecutar y que ofrezcan unos sonido ya afinados y afinados en consonancias educativas, es decir, cercanas a las exactas o naturales. Nos surgen entonces los tipos de xilófonos, marimbas, metalófonos, etc, que consisten en una serie de objetos sonoros ordenados según una escala y fácilmente accionable por precusión de una varilla, baqueta o palo. Su sonoridad duradera e independencia sonora permiten consonancias y armonías más o menos simples, incluso en las melodías, ya que las notas anteriores a la presente forman una resonancia respecto a la cual suena (consuena).

Disponemos ahora ( escribimos en la década de los 90) de una nueva gama de instrumentos: los electrónicos, que ofrecen potencialmente las cualidades que pedíamos para los instrumentos infantiles. Desgraciadamente estas posibilidades no se realizan, al menos por ahora. En efecto, por un lado, su accionamiento, simulado mediante la electrónica, no tiene las cualidades de naturalidad de respuesta que parecen necesitarse en un instrumento con el que nos expresamos (los pianistas se quejan de la falta de reacción del teclado, por ejemplo).

Por otra parte, su facilidad es excesiva. Con un pequeño toque se accionan orquestas, instrumentos de cuerda, de viento, grupos de cuerda y percusión. En fin, el niño ( y el adulto, que con frecuencia lo utiliza infantilmente) disponen de demasiado poder, como aprendices de brujo que no controlan la capacidad sonora puesta a su disposicioón.

El niño que maneja un sintetizador de ese tipo no va elaborando sus posibilidades poco a poco, aprendiendo y ordenando posibilidades tímbricas, dinámicas y rítmicas; dispone de todo desde el comienzo y probablente dserá sobrepasado por ello.

Además , la afinación de estos dispositivos es errónea, por tratarse de una escala exactamente temperada, sin las ajustes y retoques que los músicos dan a sus instrumentos y que hacen el temperamento admisible. Están perfectamente afinados segun una escala temperada y, por lo tanto, imperfectamente afinados según una escala musical (tema A.15 ).

De modo, que con reservas, porque todo es revisable, nos mostramos opuestos al empleo de estos aparatos en la iniciación musical (( más tarde será casi imposible de evitar ! ). Esto en cuanto al rasgo tono.

En cuanto a los sonidos sin tono, tanto los que podemos llamar sordos, propios de tambores, bombos, panderetas, etc, como los que tienen un timbre intermedio entre sonoro y sordos, los que hemos llamado campanales (más abajo, A.13.6.5.), nos ofrecen multitud de posibilidades, sólo limitadas por la imaginación.

Una vez salvada la etapa inicial, cuando el niño ya posee en su interior una noción del sonido musical y de la escala o escalas a utilizar, puede ya buscar esos sonidos y escalas en un instrumento de afinación variable: la Flauta de Pico es popular y útil para ello; y sus diferentes modelos y tesituras son un primer acercamiento al mundo de la armonía.

La cuerda puede venir después: la Guitarra está quizá muy ligada a tipos de música determinados, como Rock, Flamenco, Clásica, por lo que quizá debe dejarse su uso para más tarde; puede además recaerse en un mero rasgueo, lo que reduce sus grandes posibilidades.

Cuerdas de afinación enteramente variable (Violín, Cello) son difíciles de tocar y precisan un tiempo contado en años para que sean musicalmente útiles: convendrán entonces.

El Piano también puede abordarse tras la etapa preparatoria, en que sus inmensas posibilidades anegan, por decirlo así, el desarrollo perceptivo del alumno.

Existe un problema con el aprendizaje de estos últimos instrumentos: como objeto de un gran desarroollo técnico, su aprendizaje prematuro, sin dirección técnica apropiada, viciará la ejecución en aquellos que han de seguir después una enseñanza especializada. Por ello, una posible solución, compatible con la espontaneidad de la iniciación, es reservar su aprendizaje hasta que la trayectoria musical del niño se manifiesta: aquellos que van a estudiar la Carrera de Música aprenderán la técnica especializada de piano, violín, guitarra con un profesor adecuado (dentro o fuera del colegio). Los demás aprenderán libremente esos instrumentos, decantándose después por donde deseen: grupo de pop, de jazz, blues, canción melódica, etc.

Esta diferenciación no debe tener un matiz jerárquico: simplemente se aprenderán técnicas diferentes: no olvidemos que el Saxo ha sido 'descubierto' por los músicos negros de jazz desde los años 30 o 40: y lo que el instrumento es hoy a ellos se les debe, más que a su uso en la orquesta clásica. asimismo la Guitarra Flamenca, con toda su fuerza y belleza usa una técnica empírica surgida fuera de los conservatorios.

Para resumir, empezar con instrumentos simples que educan la percepción: pasar progresivamente al resto.

A.13.3. Producción del sonido en un instrumento musical

───────────────────────────────────────────────────────

Detengámonos ahora en las partes físicas de la estructura física y funcional de un instrumento de música: que contien: generalmente un elemento vibratorio que emana el sonido, y un resonador y amplificador que ampligica y filtra ( el timbre de) el sonido recibido. Esto vale para instrumentos de cuerda (cuerda y caja de resonancia) y de viento (boquilla y tubo). El elemento vibratorio es excitado a su vez por una acción humana, acorde con su naturaleza: golpe, pulsado, frotado, para cuerdas.

Soplado para viento. La naturaleza de la excitación al elemento vibratorio en el viento es más compleja: sólo soplo en fautas de pico y similares, pues el 'pito' o embocadura de esa flauta es productor directo de sonido; soplo sesgado en flauta Travesera, y de borde (como Quena india, Nai árabe, Shakuhachi japonés), o soplo y contracción elástica de los labios en los metales; o soplo y presión en maderas (clarinetes, oboes y saxos).

En la percusión el elemento vibratorio es excitado por un golpe, como su nombre indica. Esta percusión, no obstante puede ser muy diversa: con mano, con palo o baqueta, con escobilla, mazo acolchado, etc. Incluso la cuerda de piano es percutida, con un macillo acolchado.

En todos los instrumentos hay un control de uno o varios rasgos musicales para diversificar el repertorio sonoro y expresivo de la ejecución, cuanto menos rasgos y menos variables son, más primitivo resulta el instrumento y precisará generakllmente de otros a los que acompaña y con los que combina en un instrumento superior (grupo).

El tono es controlado en la cuerda bien acortándola más o menos (una sola cuerda produce varios sonidos, como violín, guitarra) o mediante varias (cada cuerda produce un sonido, o unos pocos, como el arpa). No obstante en los primeros se usan varias cuerdas porque elo timbre del instrumento varía radicalmente de larga a corta: hay que cambiar de cuerda para mantener una constancia tímbrica, y para ejecutar con facilidad

En el viento se controla el tono, bien con varios tubos afinados (flauta de pan, instrumento del afilador) o con uno que se acorta a medida; este acortamiento de realiza fácilmente mediante agujeros adecuadamente espaciados y dimensionados (maderas) o mediante tubos adicionales ( metales ). Experimentos con una combinación de ambos no han sobrevivido, como el oficleide).

El percusión se controla el tono, cuando lo hay, mediante la tensión del elemento vibratorio, generalmente una membrana elástica (usualmente circular) sujeta por los bordes.

Conviene distinguir entre el tono dado a una nota, grado o posición del instrumento, que pertenece a la escala, y aquellas variaciones más sutiles y de variación contínua, que durante la ejecución pueden servir para modificar ligeramente ese tono; entonces puede tirarse ligeramente de la cuerda, puede vibrarse el dedo que sa sujeta (vibrato), puede deslizarse (portamento) puede tensarse ligeramente. En el viento puede apretarse la embocadura, inclinar el instrumento, soplar más fuerte para modificar esa afinación durante la ejecución. Se controlan respecto a la la escala las proipiedades armónicas y tonales de la música, mientras que estas pequelñas variaciones permiten la ejecución expresiva e imaginativa, más prosódica, podríamos decir.

El timbre se varía mediante la fuerza del golpe o soplado, cambiando el lugar del golpe en la percusión, o de la pusasación y frpote en la cuerda.; el cambio de cuerda lo varía.

La intensidad, por supuesto de cambia mediante la fuerza de la excitación aunque como hemos visto, ese cambio va acompañado de cambios paralelos en los demás rasgos .

Así que en un instrumento pueden variarse los rasgos. Una vez dotado el instrumento de aquellos valores de los rasgos acordes con la cultura a la que pertenece, generalmente con sólo el repertorio de sonidos de la escala empleada, el instrumento está preparado para cooperar en esa música.

Las ideas anteriores no son novedosas en sí mismas; solamente se incluyen para mejorar la comprensión de los instrumentos que conocemos, permitir la comprensión de otros nuevos con similares principios ( por ejemplo en otras culturas) y además para permitirnos ideas de construcción propia y de los niños.

A.13.4. Instrumentos elementales

───────────────────────────

Existen instrumentos prácticamente universales:

Por ejemplo, la flauta: un tubo de caña o bambú, con agujeros adecuadamente espaciados que se sopla en un extremo, bien sobre el borde (nai) bien sobre un agujero (travesera, bien sobre una embocadura tipo pito. Hay cientos de flautas de esos tipos en todos los lugares y épocas; y en cualquiera puede construirse una, siempre que conozca el código tonal (la escala) que ha de emitir el instrumento, y el modo de hacerla sonar (véase construcción de una en apartado siguiente ).

El segundo el el rabab: un palo grueso que atraviesa un coco sobre l que se tensa una membrana y sobre la cual se coloca un puente o tablilla perpendicular. Por último se tensa una o varias cuerdas entre los extremos del palo, apoyándolas en el puente. A este principio pertenecen todos los instrumentos de cuerda pulsada y frotada, si bien la membrana y coco pueden ser una caja de madera (mucho o nada sofisticada).

La percusión es aún más libre: cualquier objeto puede sonar adecuadamente si se lo golpea o acciona adecuadamente. Cacharros de cocina de metal o barro, objetos de metal de mil formas y usios, macizos o huecos de madera, plástico, cartón,: todo suena en un mundo sonoro e incluso ruidoso.

A.13.4.1. Construcción de una flauta en el Aula.

────────────────────────────────────────────

La construcción de una flauta por los niños les acercará al instrumento, comprenderán su mecanismo y función; y podrán además hacer música bonita y creativa. Síganse los pasos sobre la figura A.13.1.

1. Materiales

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Una caña de unos 20 o 30 centímetros y de 1 y medio de diámetro exterior, aproximadamente. Mejor de un sólo nudo.

Un trozo de madera o tapón.

2. Herramientas

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Una navaja, con punta.

Una varilla larga (como aguja de coser)

3. Construcción

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

a. Se corta la caña con la navaja (( cuidado!) entre dos nudos, formando un tubo. Si no es suficientemente larga se usan dos nudos agujereando la división con la varilla; si no cede, se calienta al rojo (( cuidado !).

b. En el extremo opuesto se corta el 'pito'. Véase figura adjunta.

b1. Se reduce el tapón hasta que entre ajustado en el tubo de la caña. Se corta en él además, un segmento circular de modo que deje una rendija al entrar en el tubo.

b2. Se cortan ambos de manera diagonal.

b3. Se hace un agujero cuadrado con una pared a ras del tapón interior. La pared del agujero opuesta a la anterior se corta en forma inclinada, de bisel.

b4. Se adelgazan los bordes de la boquilla para más capacidad.

c. Se agujerea la flauta, con la punta de la navaja ((cuidado!).

c1. Se toma la distancia entre el agujero de la boquilla y el otro extremo. Se divide en 13 partes, que marcaremos con 13 rayas. También se han podido tomar 26 cm. y añadir otros dos para el pico. Así tenemos agujeros cada 2 cm.

c2. Contando desde el extremo opuesto a la boquilla, agujereamos las marcas 2, 3, 4, 5, 6, 7, y 8, es decir, 7 agujeros. Los 4 de abajo para los dedos de la mano derecha. Los 3 de arriba para los de la izquierda (excluido el meñique).

c3. Entre los dos últimos hacemos otro agujero, en la parte opuesta de los demás (para el pulgar de la izquierda). Está pues en el punto medio entre el agujero del pito y el primer agujero (meñique de la derecha).

Interpretación.

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Soplar en la boquilla de pito.

Se busca la escala mayor a partir de la nota con todos tapados, que llamaremos DO. Se asciende grado a grado destapando uno a uno los agujeros, excepto el FA, que tapa 2 y 4, y Do agudo, que tapa 6, destapando 7.

La octava aguda se consigue soplando más fuerte y/o destapando el agujero del pulgar.

Mejorar la afinación buscando los intervalos simples, como quintas y cuartas. Si es necesario acortar ligeramente el tubo por el extremo inferior. Ajustar el diámetro de los agujeros si procede.

Variantes.

‑‑‑‑‑‑‑‑‑

Puede soplarse sobre el borde del tubo cortado a ras por el agujero de la boquilla o pico, como las flautas árabes y persas, aunque es difícil conseguir sonido (hay que silbar sobre el borde).

Si se hace una muesca, se sigue el procedimiento de la Quena peruana o la Flauta japonesa.

Pueden también evitarse los agujeros colocando otro tubo (caña) exterior y ajustado al primero; corriendole sobre él, como un trombón de varas, subirá y bajará la altura tonal; habrán de buscarse los grados con cuidado, pero el efecto será muy expresivo.

Por último, puede emplearse la boquilla representada a la derecha, un simple tramo fino de caña, donde se tractica una incisión diagonal; se introduce en el tubo, ajustadamente. Al soplar dejando dentro de la boca esa boquilla, se produce un sonido untuoso y muy interesante; es el principio del clarinete. Se emplea en instrumentos folklóricos españoles.

A.13.5. Instrumentos folklóricos.

────────────────────────────────

El folklore musical ofrece una multitud de instrumentos muy apropiados a la iniciación y cultivo primero de la instrumentación.

Los instrumentos de aula, tipo Orrf son muy interesantes, es verdad: pero significan una búsqueda de 'naturalidad' en un pais muy cultivado y desarrollado, lo que significa una paralela pérdida folklórica (en Baviera el folklore es casi orquestal). Nuestra situación en muy otra: por una parte poca formación musical media, lo que, si bien se pretende corregir ahora, ha significado también una parcial conservación de melodías, géneros e instrumentos autóctonos.

Además el pasado histórico español consta de tantas etapas influencia y variantes, que la riqueza y variedad de su folklore es muy grande. Griegos, Romanos, Cartagineses, Visigodos, Arabes

orientales y norteafricanos han traído y desarrollado aquí sus músicas e instrumental (solo en la época árabe de España, el Andalus, había más de cincuenta instrumentos diferentes ).

Aún ahora de emplean muchos instrumentos no cultos o semicultos: entre los primeros estrán el Chistu y Tamboril, pais vasco; la Gaita y Panderos Cuadrados en Galicia. La Zanfoña, en el norte. Hay Dulzainas tipo oboe en Valencia, Cataluña, Castilla (en Cataluña de tipo semiculto, como la Tenora). Percusiones varias, como las Castañuelas o Palillos, la Caña Partida en Andalucía; Tambores, Panderos y Panderetas en todo el país. Entre los semicultos están el Acordeón, muy en país vasco, y los Instrumentos de Púa, como Bandurrias y Laúdes. La Guitarra está omnipresente, con una técnica simple.

Si salimos fuera de nuestro país, nos encontramos con la Guitarra Portuguesa, las Darbukas (tambor de barro en forma de copa; véanse instrumentos árabes de percusión en A.5.5.12), Rabab (violín de un sólo cuerpo), Nai (flauta de bisel), el 'Ud (laud de cuello corto) en Marruecos. Kueitra (laud de mango largo) en Argelia. Salterios en Europa Central‑Meridional y en Cercano oriente (qanun y santur). Flautas y dulcimeres hacia Escocia e Irlanda. En Méjico, decenas de flautas de barro, tambores varios. En India, cientos de instruementos floklóricos además de los cultos.

En fin, hay miles de instrumentos simples utilizados por los folklores del mundo que pueden ser adecuadamente usados en la iniciación musical. En nuestro país disponemos de muchos y de otros ahora olvidados (como el alboque) que pueden (deben) ser usados en nuestras aulas infantiles. Pueden pues constituirse grupos con estos instrumentos que cubran las necesidades educativas de los niños españoles; y esto dentro de las peculiaridades de cada nacionalidad (Euskadi, Catalunya, Galicia, Andalucía, Baleares, Canarias, etc.).

A.13.6. Producción del sonido musical.

───────────────────────────────────────

Aunque como hemos visto, todos los sonidos pueden ser empleados musicalmente, son considerados como tales tradicional y especialmente aquellos dotados de tono (altura tonal). Nos proponemos ahora revisar con algo más de detalle, en que consisten esos sonidos y sobre todo, sus intervalos, de los que se deducen los inmensos edificios de la Melodía, la Modalidad y la Armonía.

Para ello es indispensable revisar algunos conceptos y definiciones de base.

A.13.6.1.Tiempo, Vibración y Frecuencia.

───────────────────────────────────────────

Medimos las duraciones en segundos o fracciones de él, como décimas, centésimas o milésimas (milisegundos). Para sucesos más largos se emplean minutos y horas. No suele haber fenómenos musicales que precisen unidades mayores.

Definimos la frecuencia como Repeticiones por unidad de tiempo. Frecuencia es pues velocidad de Repetición.

Por ejemplo, la notacion usual del metrónomo, o┤ = 60 significa repeticion de una blanca 60 veces en un minuto. La frecuencia de un Tono se mide en Vibraciones por segundo o Hercios, siendo una vibración un movimiento de ida y vuelta repetido (es la vibración de un cuerpo físico quien produce un sonido, midiéndose su tono en las mismas unidades). Se adoptó como La el sonido producido por un cuerpo físico que vibra 440 veces ( de igual duración) en un segundo.

Llamamos precisamente Período a la duración de 1 vibración. Se ve que período y frecuencia son conceptos correlativos que verifican:

f = 1 / T T = 1 / f

Si un suceso se repite cada décima de segundo ( periodo = .1 seg.),su frecuencia es 10 veces por segundo ( f = 10 = 1/.1)

Suele decirse que período y frecuencia son inversamente proporcionales (cuando uno se duplica pasa el otro a su mitad).

El modo más simple y natural de vibrar, o sea, de repetir un movimiento de vaivén, es la llamada forma Senoidal, en que el alejamiento y del punto de equilibrio sigue una ley definida por la función:

y = seno ( t )

siendo t el tiempo. Esta función puede definirse como la proyección (la 'sombra') sobre un diametro de un punto que gira sobre una circunferencia con velocidad constante. La proyección convierte un giro en un vaivén o vibración. Los valores máximos del alejamiento citado son 1 y ‑1, si era 1 el radio de la circunferencia. En la figura adjunta vuelve a pasar por el mismo lugar cada 6 segundos aproximadamente (6.28=2Ò). Se observan varias simetrías y parecidos en la curva.

y ┤ y= sen (t)

1 ┤ . .

┤ . . .

┤ . .

─.────────┬────────.────────┬────────.───────

┤ 2Ò/4 2Ò/2 3.2Ò/4 2Ò

┤ . . t

. . .

┤ . .

La función siguiente, muy relacionada con la anterior, presenta una amplitud A y un período T, ya que su valor se repite cada T segundos (compruébese), y comienza en una posición negativa para el momento inicial, t=0.

y ┤ y=A¨sen(2Ò(t‑þ)/T)

A ┤ . .

┤ . . .

0 ────.────────┬────────.────────┬────────.───────

┤ . T/4 T/2 3T/4 T

┤ . . . t

. .

┤ . .

Podemos considerar esta funcion seno ampliada como la proyección sobre el diámetro del movimiento de un punto que se mueve sobre una circunferencia de radio A con velocidad de 1 vuelta cada T segundos, y que comienza a moverse desde un punto inicial 'atrasado' de þ segundos. Se le llama a þ la Fase.

Amplitud, Frecuencia y Fase definen completamente una senoide, es decir, puede saberse la posición de la ordenada y para cualquier momento (valor de t). Véanse dos senoides en la fig. A.13.2

Dos Senoides, representación de movimiento vibratorio simple, o sonido puro. La primera de gran amplitud. La

segunda de pequeña.

En la primera se ven 5.25 períodos, en la segunda, casi 10.

Si la anchura del papel representa 10 milisegundos, entonces la frecuencia de la primera es:

5.25/(10/1000) = 525 vibraciones por segundo o hercios.

La de la segunda es:

10/(10/1000) = 1000 hercios.

fig. A.13.2 A.13.6.2. Funciones Periódicas, Espectro y Descomposición de Fourier

───────────────────────────────────────────────────────────────

En general, una función periódica es aquella que se repite igual a sí misma a intervalos iguales de la variable (tiempo en nuestras aplicaciones); estos intervalos iguales son el período, T. Es decir

f(t) = f(t+T) para cualquier t

Por ejemplo, el seno es una función periódica de período 2Ò, como veíamos antes; pero hay otras, en número infinito, que lo son también, como la de la fig. A.13.3.

fig. A.13.3.

Pero no, en cambio, la de la fig. A.13.4.

fig. A.13.4.

Ya se ve que todos los múltiplos del período T son también períodos, por lo que reservamos el nombre de período para el menor (máximo común divisor) de todos ellos.

Cualquier función periódica puede expresarse como suma de varias senoides de amplitudes y fases variables, y cuyas frecuencias son todas múltiplos de una, llamada Fundamental o Primer Armónico, frecuencia que es igual que la de la función analizada. Esta afirmación, que no probamos aquí constituye el llamado Teorema de Fourier, y el conjunto ordenado de esas senoides, la Serie de Fourier.

La adición de más y más armónicos (múltiplos de la frecuencia del fundamental) no hace más que complicar, rizar, sacar picos en esa forma de onda, pero no altera su período. Por ejemplo la siguiente forma de onda de período T, en la que se percibe la repetición de la forma de onda a partir del instante t=T:

y ┤ una suma de armónicos de f=1/T

A ┤

┤

┤ . .

┤ .. . . ..

┤. .. . . . ..

0 .──────.──┬─.─ ─── ───.─────┬────────.──────.─

┤ .T/4. T/2 3T/4 T

┤ .. . . t

┤ . .

podría tener un espectro como el de la figura síguiente.

Este fundamental y varios de sus armónicos pueden faltar pero siempre la suma de los demás armónicos tiene un período igual al de esa función (siempre que haya al menos dos).

El espectro es la representación de una función, llamada 'en frecuencia', en la que las alturas u ordenadas de los puntos representan la amplitud de la correspondiente componente de frecuencia en abscisas.

El espectro de una función periódica es, por el teorema de Fourier, del tipo peine, como presenta la figura siguiente.

Se ve que el armónico más importante, intenso, es el 2, que el 7 falta, y que las intensidades van decreciendo al crecer el orden de armónico, desapareciendo a partir del 14.

A │

m ┤ │

p ┤ │ │ │ │

l ┤ │ │ │ │ │

i ┤ │ │ │ │ │

t ┤ │ │ │ │ │ │ │

u ┤ │ │ │ │ │ │ │ │ │ │

d └───┴───┴───┴───┴───┴───┴───────┴───┴───┴───┴───┴───┴─

1 2 3 4 5 6 7 8 9 10 11 12 13

número de armónico frecuencias

Espectros peine de una vocal, la /e/., para dos frecuencias fundamentales (tono), baja y alta, donde pueden verse los armónicos del fundamental y su importancia relativa. El timbre de /e/ es debido a la presencia de armónicos fuertes en las zonas de 400 hz. y 2200 hz, correspondientes en el primer caso a los armónicos 2,y 9‑10‑11, mientras que en el segundo correponde a 2‑3‑4, y 11‑15.

fig. A.13.5

Las funciones períodicas son importantísimas en música, debido a que presentan para la audición un carácter fundamental: son percibidas como dotadas de tono (pitch), rasgo sobre el que se han construído las escalas, armonías, etc.

Véanse en las figuras A.13.5 los espectro peine de una vocal, la /e/.

El aspecto tímbrico, importantísimo también en música, como es evidente, será tratado en cursos posteriores.

Las señales verdaderamente interesantes para la música son las Señales Pseudoperiódicas, o aproximadamente periódicas en un cierto intervalo de tiempo. Con ellas se construyen gran parte de los sonidos musicales y se edifican las relaciones tonales que constituyen parte tan importante de la música. En lo que sigue, cuando hablemos de frecuencias y sus relaciones, nos referiremos siempre a esta psudoperiodicidad o periodicidad limitada.

Las funciones aproximadamente periódicas, o Psudoperiódicas, que definimos como las casi periódicas en un cierto intervalo de tiempo:donde se aprecia el tono ascendente y sus armónicos, que ascienden con su fundamental.

periódicas pseudoperíodicas

f(t) = f(t+T) para todo t f(t) = f(t+T) + e para t en I

donde e es una cantidad pequeña en relación con los valores de la función: es decir el carácter períodico que se aprecia a ojo cumple estas condiciones.

Véanse la figura A.13.6 el espectro que evoluciona en tiempo de un sonido puro en un glissando ascendente y descendente: el tiempo va de abajo arriba en esta representación.

En la figura A.13.7 se ve la forma de onda de varias notas cantadas sucesivas y su correspondiente espectro evolutivo,

Espectro que evoluciona en tiempo de un sonido puro en un glissando ascendente y descendente: el tiempo va de abajo arriba en esta representación.

A.13.6

Forma de onda de varias notas cantadas sucesivas y su correspondiente espectro que evoluciona. Se aprecia el tono ascendente y sus armónicos correspondientes, también ascendentes.

El tiempo va de abajo arriba.

A.13.7

A.13.6.3. Cuerdas y Tubos

────────────────────────────

Estos sonidos periódicos son producidos en la práctica por dos tipos de elementos vibrantes: la Cuerda y el Tubo. Ambos son elementos largos, es decir, en los que predomina una sola dimensión.

Ambos elementos vibrantes se diferencian en el modo de vibrar: mientras las cuerdas lo hacen transversalmente (perpendicularmente a la cuerda) en el tubo la vibración en longitudinal ( a lo largo del tubo). También hay que decir desde ahora que lo que vibra en un tubo sonoro no es el tubo, sino el aire contenido en él.

Las cuerdas al vibrar, producen un espectro o suma de armónicos, cuya importancia o intensidad relativa depende de la forma de excitación y del material; su fundamental, el primer armónico, y todos los demás, múltiplos de él, tienen una frecuencia que depende de las dimensiones de la cuerda, longitud y grosor, de su tensión, y de su material ( su densidad).

La expresión que liga estas variables es

┌─────

1 │ T

F1 = ──── │ ────

2AL o D

de modo que, si medimos la longitud en metros, la tensión (fuerza) en newtons y la densidad lineal (masa por unidad de lingitud) en kilos por metro), obtenemos la frecuencia en hercios, vibraciones por segundo. Así, la frecuencia emitida es mayor si disminuimos la longitud, la sección y la densidad, y si aumentamos la tensión.

Los armónicos de esa cuerda tendrán frecuencias doble, triple, cuadruple, etc.

El aire de un tubo fino vibra longitudinalmente, no desplazándose de un lado a otro, como la cuerda, sino comprimiéndose y expandiéndose, hecho posible para todos los gases.

Las frecuencias de vibración de un dependen sobre todo de su longitud, de la velocidad de propagación del aire, y desde luego que esté cerrado o abierto.

Para el tubo cilíndrico abierto por ambos extremos la expresión es:

F1 = ────

2AL

expresándose c en metros por segundo, y L en metros.

Los armónicos;

F2 = 2AF1, F3 = 3AF1, F4 = 4AF1, F5 = 5AF1, etc

El Tubo cerrado por un extremo, en cambio, presenta un armónico primero o fundamental una octava más baja que la del abierto de igual longitud:

F1 = ────

4AL

expresándose c en metros por segundo, y L en metros.

Además, en este caso sólo aparecen los armónicos impares:

F3 = 3AF1, F5 = 5AF1, etc

Este es el caso del Clarinete, cuya ausencia de armónicos pares es percibida como sonido 'hueco'. También se parece al tracto vocal en la voz humana (tema A.12) a la cual dicen que el clarinete se parece.

Los agujeros de un tubo lo acortan parcialmente, es decir no tanto como si se cortara realmente por el agujero.

A.13.6.5. Sonidos sin Tono.

─────────────────────────

Si los armónicos de un sonido no son múltiplos de uno de ellos, ya no hay armónicos: se llaman parciales. Si estos parciales son pocos, frecuencias puntuales, el oído reconoce a estos sonidos iuna cierta calidad que sin ser tonal, no es tampoco sorda, como un ruido. Estos sonidos son llamados Campanales, por ser la campana uno de sus representantes más eminentes. Otros es el Gong, los Cencerros, etc. La Celesta está en el límite, pues se reconoce el timbre campanal junto con una afinación tonal.

Los Ruidos tienen un espectro de tipo continuo, es decir, hay miles de frecuencias juntas sin relaciónes numéricas sencillas unas con las otras.( fig. A.13.3)

A.13.7. Intervalos del Tono.

───────────────────────────────────────────────────────────────

SE expresa una agregación de tonos o notas, citando sus frecuencias en cualquier orden, por ejemplo, creciente:

(400,500,600) hercios

Maneras alternativas de expresarlo son el citar una frecuencia de base (por ejemplo la menor) y las relaciones de frecuencia de las demás con ella:

400 * (1, 1.25, 1.5)

Si las frecuencias son múltiplos enteros de alguna dada, podemos expresarlas mediante esa frecuencia divisora y los múltiplos correspondientes, evitando así números fraccionarios:

100 (4,5,6)

La manera más sencilla y exacta de expresar un intervalo es pues citar las frecuencias de dos tonos que lo componen, en forma de pareja: intervalo (440,450). Podemos hablar, pues, del intervalo (100,200), que queda así determinado.

Pero esto no resulta satisfactorio porque alude a los extremos del intervalo, pero no a su tamaño, a la distancia entre ellos. No permite comparar esa distancia con la de otros dos frecuencias, por ejemplo (200,400), que sin embargo, resulta perceptivamente igual a la anterior (lo que llamamos una octava en música). )que haremos para que ambos intervalos sean iguales, en efecto?. Su diferencia no nos vale ya que es el doble en el segundo caso: 200‑100 y 400‑200.

Para medir pues estos intervalos y reflejar en esta medida esa igualdad perceptiva de relaciones entre intervalos , se hace necesaria una manera de expresar esa semejanza entre una misma relación de frecuencias, tanto cuando las frecuencias son bajas como cuando son altas. El cociente cumple esta propiedad, ya que intervalo(440,880) = intervalo(220,440) = 2/1.

Esta fracción, 2/1, es pues una medida de la llamada (por razones que veremos al hablar de las escalas) octava. El intervalo descendente será expresado por el quebrado inverso, 1/2.

La representación de intervalos musicales mediante fracciones racionales tiene por lo menos dos importantes razones tradicionales: primeramente, que fue la unica manera conocida por los antiguos de obtener y recordar un intervalo: dividir una cuerda en determinado numero de partes iguales y tomar cierto numero de ellas.

Puesto que la frecuencia de vibración de una cuerda (medida en vibraciones por segundo, vps) es inversamente proporcional a su longitud, el cociente entre la frecuencia de la cuerda completa, y la de la cuerda acortada, intervalo ascendente, vendra dada por el cociente entre número total de partes y porción de partes tomada, fracción mayor que la unidad.

frecuencia = F longitud = 3L

<‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑'‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑'‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑<

<‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑'‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑<

frecuencia = (3/2) F longitud = 2L.

La otra razon, relacionada con la anterior, es que solo han sido considerados tradicionalmente como consonantes los intervalos así obtenidos, y de ellos sobre todo los del tipo (n+1)/n, con n creciente, o sea 2/1, 3/2, 4/3 etc (lo veremos en las páginas siguientes).

Por lo tanto, en esta representacion, los intervalos ascendentes son fracciones mayores que la unidad, numerador mayor que denominador, los descendentes fracciones menores que la unidad, numerador menor que denominador. Si habláramos de longitudes, todas las fracciones serian las inversas, pero nos atendremos desde ahora a frecuencias.

Conocida la frecuencia en vps (vibraciones por segundo) es sencillo encontrar la de la nota que forma con ella determinado intervalo: basta multiplicar dicha frecuencia por la fracción racional que expresa el intervalo. En efecto, como

f2 a a

── = ── entonces f2 = f1 ¨ ──

f1 b b

así, si el La3 tiene 440 vps, el Si3, a un tono superior, tendrá 440 x 9/8 = 495 vps.

)Problemas de esta medida de intervalos por fracciones? Que no permite una comparación cómoda de intervalos: ) quien es mayor, 6/5 o 40/27? Deberemos pasar a común denominador para comprobar que 162/135 es menor que 200/135. Además la composición o suma de intervalos requiere productos y cocientes no cómodos de manejar.

Podemos también entonces realizar la división y obtener el número fraccionario cociente: obtendremos que 6/5=1.2 es menor que 40/27=1.48. Pero esta medida, el cociente de frecuencias, no resulta idónea: en primer lugar el intervalo descendente (igual en tamaño, pero en sentido contrario) es expresado con un número que no se parece al anterior, es su inverso. La octava descendente es 100/200 = 1/2= .5 y la ascendente 2. Para (300,200) tenemos 1.5 y .6666666... etc.

Esto nos obliga a pasar contínuamente de quebrados a decimales y viceversa, lo que es engorroso. Ya veremos como la introducción de la medida logarítmica resuelve estos problemas (pagando un precio, como siempre).

A.13.7.4. Armónicos y Espiral armónica

────────────────────────────────

Según sabemos, un sonido con tono (los ruidos son sonidos sin tono), puede ser considerado como una suma de vibraciones simples, de tipo senoidal, cuyas frecuencias son todas múltiplos de una, llamada fundamental. Estas frecuencias son llamadas armónicos, siendo el fundamental el primero, y pueden ponerse de manifiesto en una cuerda o tubo sonoros. Representando los intervalos con el fundamental mediante el cociente o razón de sus frecuencias obtenemos la serie de intervalos:

1/1 2/1 3/1 4/1 5/1 6/1 7/1 8/1 9/1 10/1

11/1 12/1 13/1 14/1 15/1 ...

Si, por ejemplo, el fundamental son 100 hz. (un hercio es una vibración por segundo), los armónicos serán 200, 300, 400,..etc hercios.

Vamos a representar estos armónicos a lo largo de una línea de modo que su distancia sobre ella sea su diferencia en hercios, es decir, constante, y, por otro lado, su situacion angular, es decir, el ángulo que forma el radio que pasa por el punto del armónico y el que pasa por el punto correspondiente al fundamental, represente el intervalo con ese fundamental, correspondiendo una vuelta completa a la octava. Se obtiene así una espiral que llamaremos la Espiral Armónica. Véase esta espiral en la figura A.13.8.

Otra propiedad de esta espiral consiste en que la distancia de un punto de ella al centro es proporcional a la medida absoluta de la frecuencia: si el punto de partida representa 100 hz y dista 1 cm del centro, entonces un punto que diste 3 centímetros representa 300 hz.

Numeramos cada armónico según su orden asignando el 1 al fundamental, que llamamos primer armónico. Se observa cómo todos los armónicos separados por octavas, por ejemplo, la serie 2,4,8... o la 3,6,12,.. se encuentran sobre un radio que parte del centro.

asimismo se ve que en cada vuelta de la espiral de duplican en número de armónicos, intercalándose los nuevos (en una octava) entre los antiguos. Por ejemplo, entre los armónicos 16 y 18, octavas de los 8 y 9, se intercala el 17, sin correspondiente en la vuelta anterior, pero sí en todas las su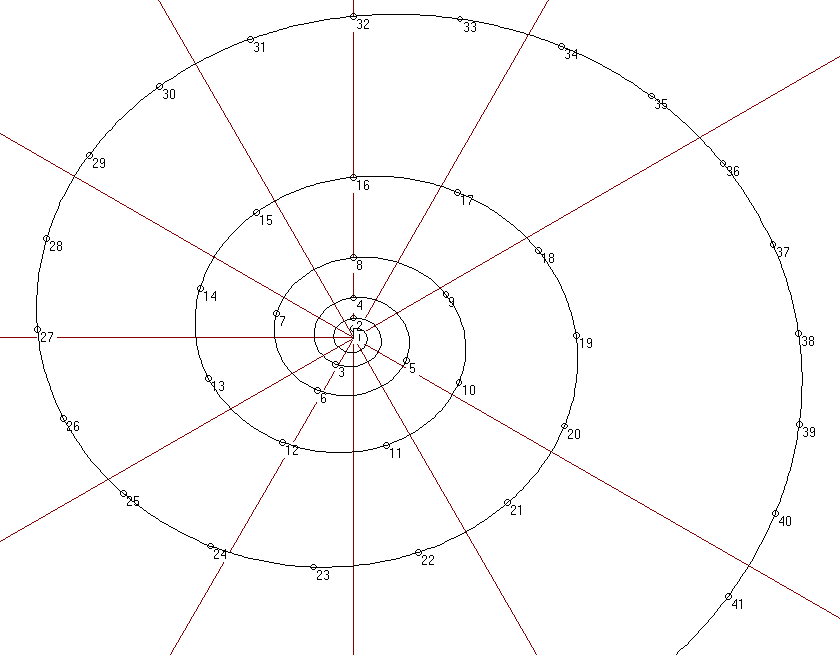

cesivas.

La Espiral Armónica

fig. A.13.8.

A.13.7.5. Intervalos Naturales

────────────────────────

El primero y segundo armónicos están muy emparentados entre sí en la percepción: son 'el mismo' en cuanto que dos melodías separadas por ese intervalo suenan 'igual' y son empleadas de manera quizá espontanea por hombre y mujer cantando juntos ( a veces emplean la quinta, que ahora veremos).

Inmediatamente se perciben como vecinos al fundamental el tercer armónico, razón 3/1, y su octava inferior, llamada quinta ( razón 3/2); entre el tercero y cuarto armónicos existe el intervalo 4/3, llamada cuarta, etc. Todos lor armónicos contíguos forman entre sí razones de la forma (n+1)/n, intevalos que recibieron el nombre de supernumerarios.

Todos estos intervalos de producen, como se ve, en la vibración natural de algunos cuerpos, por ello los llamaremos naturales. Sin embargo no dejamos de reconocer que en la naturaleza se producen otros intervalos muy diferentes, entre los parciales de un cuerpo vibratorio, como en todos los cuerpos de dos o tres dimensiones (membranas, placas, campanas, etc.) o incluso de una, como en el caso de barras finas y rígidas. Dejaremos para más adelante la consideración de intervalos entre estos parciales no armónicos) y nos centraremos en los parciales armónicos, base de la inmensa mayoría de la música que conocemos en los tres últimos milenios.

La importancia de estos intervalos naturales reside pues más en la sencillez perceptiva o consonancia, que en su naturalidad física. En el capítulo 3 veremos las escalas construídas con ellos

A.13.7.6. Medidas Logarítmicas de de Intervalos. El Cent

─────────────────────────────────────────

Vamos a mostrar ahora que tanto la percepción de los intervalos como el lenguaje habitual en la música miden los intervalos en forma logarítmica. Veamos también que medidas y operaciones resultan así lógicas e iluminadoras. El logaritmo parece 'comportarse como la percepción', el oído en este caso (en una primera aproximación).

Existe una manera de conseguir un número igual para intervalos ascendentes y descendentes? Sí, el logaritmo, puesto que sabemos que log(a/b)=‑log(b/a), Así que el logaritmo del cociente de frecuencias resuelve nuestro problema. Por otra parte la composición de intervalos queda expresada en forma muy sencilla, según veremos en el siguiente párrafo, pero antes desarrollemos la idea anterior para conseguir medidas útiles de intervalos.

Propongamos una expresión general de esa medida logarítmica y determinemos sus constantes según nuestras necesidades:

MLI = K ¨ logA ( f2/f1 )

siendo MLI la 'medida logarítmica de intervalos' A la base del logaritmo y K una constante arbitraria.

Veamos que nosotros también utilizamos esa fórmula en el lenguaje habitual de la música, ligado a la percepción, y cómo. Si queremos medir en octavas, diremos que 1 = K ¨ logA (2), pues el cociente de frecuencias es 2/1 para la octava. Podemos elegir ahora K y A como queramos, para que se verifique la igualdad; si elegimos la constante K=1 por sencillez, tenemos que 1= logA(2): y la base A debe ser 2, porque solo 2 elevado a 1 es 2 (definición de logaritmo). Así que para medir en octavas, K=1 y la fórmula general de la MOI (medida en octavas de intervalos) queda en la forma:

MOI = log2(f2/f1)

Por ejemplo la doble octava 4/1 da log2(4)=2 (por definición de logaritmo). Pero como el logaritmo en base 2 no está disponible en las máquinas y calculadoras habituales, pasaremos a logaritmos más usuales, como el neperiano (base e=2.7...) o el decimal, base 10. Eligiendo el primero tenemos, para la medida en octavas que 1=Ko¨ln(2) , o sea, la K para octavas, K0 = 1/ln(2) = 1.4427 (operado con calculadora); entonces, en general, la medida en octavas del intervalo entre f1 y f2 es:

MOI = 1.4427¨ln(f2/f1)

En general, para otros intervalos unidad:

MLI = K ¨ ln(f2/f1)

Si queremos medir un intervalo en , por ejemplo, semitonos temperados, de los que hay 12 en una octava, la constante deberá ser entonces 12 veces mayor que para la medida en octavas; y lo mismo para otras divisiones de la octava. Realicemos entonces un cuadro útil en el que se exponen diferentes unidades de intervalo y las constantes correspondientes para la fórmula anterior:

──────────────────────────────────────────────

intervalo por octava cents constante K

──────────────────────────────────────────────

octava 1 1200 1.4427

semit.temperado 12 100 17.31

coma hölder 53 22.7 76.46

doceavo de tono 72 16.7 103.6

savart 301 3.9 434.3

Udx7‑II 1024 1.2 1477

cent 1200 1 1731

turco 10200 .11 14715

El cent se explica más abajo.

El cuadro necesita algunas explicaciones: la primera respecto al savart, unidad usada en Francia, y definida como MS=1000¨log10(f2/f1); así que hay 1000¨log10(2) = 301 intervalos savart en una octava, y, por lo tanto la constante Ks obtenida es entonces (Ks es K para savart): Ks=Ko¨1000¨log10(2)=434.3.

La coma Hölder resulta útil porque suele reflejar bastante bien loa matices de afinación usados en diferentes músicas y escalas. Está cercano a la discriminación del oído en la música real. Elaboraremos más adelante una notación basada en ese intervalo.

Udx7‑II es la unidad de medida del intervalo tonal en el sintetizador dx7‑II de Yamaha. Se incluye aquí por ser el único aparato comercial y popular que admite afinación independiente para cada tecla (se escribe esto a finales de 1989). Este teclado divide la octava en 1024 partes (2^10), potencia de 2 acorde con el carácter binario de toda la informática. El semitono queda entonces equivalente a 85.3 udx.

Conviene adquirir una idea práctica, intuitiva, del tamaño relativo de estos intervalos; por ejemplo es muy fácil comprobar, aplicando las fórmulas y tabla anteriores, que una octava (2,1) contiene algo menos de 6 tonos diatónicos (9,8), que una quinta justa (3,2) contiene menos de 7 semitonos naturales (16/15) y algo más de 7 semitonos temperados, que un tono diatónico contiene unas 9 comas hölder, que una coma holder son unos 22 cents y una tercera mayor natural (5,4) son 386 cents, contra 316 de la menor (6,5). Un semitono temperado cotiene 100 cents, lo que no es extraño si sabemos que el cent se ha definido precisamente de esta manera.

Conviene advertir que una división de la octava en partes iguales o desiguales no presupone necesariamente una escala: más bien se trata de disponer de un número limitado de tonos, de los que pueden entresacarse los grados de esa escala.

La MCI (medida en cents de intervalos) que emplea como unidad el Cent, o centésima parte del semitono temperado, es la principal de las unidades pequeñas de intervalo, y será utilizado en general en lo que sigue.

Por definición, una octava tiene 1200 cents, y en general, la medida de un intervalo (f2,f1) se obtiene mediante la expresion:

MCI = 1731.ln(f1/f2).

donde f1/f2 es la relación de frecuencias citada, y 'ln' el logaritmo neperiano.

La formula inversa nos ofrece la fracción correspondiente, conocida la medida MCI en Cents:

f1 (MCI/1731)

──── = e

La octava son pues 1200 cents, la quinta justa, 702, la cuarta justa 498; la coma Hölder, 22.6, el semitono pitagórico 90, el semitono temperado, por definición, 100, el natural, 112; el tono menor 182, el temperado 200, el mayor 204, etc.

La fórmula anterior nos permite resolver el sencillo problema de conocer la frecuencia de una nota a un semitono temperado del LA3, por ejemplo: como esta nota tiene una frecuencia f1 de 440 hz, y un semitono temperado son 100 cents, tenemos que

100/1731

f2 = f1 ¨ e = 466 hz.

El cent es una medida excelente por tener un tamaño cercano a la discriminación tonal absoluta del oído; es dificil distinguir dos tonos separados por un solo cent, y 2 son apenas distinguibles.

Véase el cuadro anteriorque incluye la medida en cents de cada intervalo:

A.13.7.7. Afinación absoluta y relativa basada en el semitono temperado

─────────────────────────────────────────────────────────────────

Este sistema musical, vigente ahora en todo el mundo, toma una nota (frecuencia) de referencia y construye a partir de ella dos sucesiones de frecuencias tales que su razón es el semitono temperado ( 1.059, 6%) y su diferencia en cents, 100, por definición. Aparecen pues 12 notas por octava, extendíendose la tesitura total en un rango desde unos 33 hercios hasta unos 8000; este límite lo fija la percepción de tono; por encima de esta frecuencia se percibe solo un silbido (algunos instrumentos se extienden aún más, no obstante).

Obtenemos así un rango útil de tonos deunas 8 octavas.

33‑ 65 ‑ 130 ‑ 261‑520‑1040‑2080‑4160‑8320‑

1 2 3 4 5 6 7 8

El sistema de notación es tradicional y utiliza los conocidos símbolos siguientes:

do re mi fa sol la si

c d e f g a b

en los países de influencia latina (arriba) y los de influencia anglosajona (abajo). Se nota que los primeros comienzan por una referencia do, que corresponde al tercero de los segundos, los cuales comienzan por a ( el sexto de los primeros).

)A qué frecuencias corresponden estos nombres?. Esto ha cambiado a lo largo de la historia, generalmente subiendo poco a poco la frecuencia (más de un tono, 204 cents, en varios siglos). Actualmente se adopta, al menos de palabra, la referencia la=440hz. lo que no obsta para que instrumentos modernos se afinen más y más altos. Tras comparar los sistemas francés, americano y de piano, elegimos el que consideramos más generalizado en nuestro ambiente, asignando 440 hz. a la octava 3; de modo que :

Diapason: LA 3 = 440 hercios.

las demás notas quedan inmediatamente fijadas por ese La 3. Admitiendo los valores teóricos de los intervalos, obtenemos el cuadro adjunto.

En realidad estos valores son solo aproximados: en efecto, el oido precisa intervalos mayores que los teóricos para la sensación correspondiente. Podemos pues añadir unos 5 cents por octava en las centrales y bastante más en las extremas. De modo que la separación real entre dos notas separadas por 6 o 7 octavas es al menos 100 cents mayor que la teórica (piénsese la importacia de este hecho, generalmente ignorado por los afinadores, constructores y usuarios de sintetizadores electrónicos).

A.13.7.8. Afinación absoluta y relativa basada en la coma Hölder

─────────────────────────────────────────────────────────

Para representar con más precisión los matices de afinacion de escalas tradicionales, no cubiertos por la nomenclatura anterior, es necesario disponer de divisiones más finas. La notación que adoptamos es la basada en la división de la octava en 53 partes iguales, iguales a la coma Hölder, como es sabido: con un error menor un par de cents quedan aproximadamente reflejados los intervalos de las escalas habituales: las mayores pitagórica y temperadas aparecen sin alteraciones, la natural de Zarlino con la tercera, sexta y séptima una coma bajas (‑),etc. La escala de referencia es, con un ligero error (1.5 cent, max) la escala pitagórica o de quintas (véase esta escala en el el tema 3).

Las desviaciones con respecto esta escala de base se expresan mediante el número de comas que se suben o bajan, segun la lista que sigue:

comas sube baja

1 + ‑

2 ++ =

5 b

Así cubriremos todas las notas; por ejemplo en los tonos:

notas: do do+ do++ reb‑ reb reb+ reb++ re= re‑ re

comas: 1 2 3 4 5 6 7 8 9

y en los semitonos:

notas: mi mi+ fa= fa‑ fa

comas: 1 2 3 4

quedando similarmente representadas las demás. Esta notación es similar, pero no idéntica a la usada por Danielou [10], y, por otra parte, la música turca tradicional [17],[30]. La notación del primero, muy precisa, resulta algo enrrevesada, al utilizar una escala de base de Zarlino, con tonos mayores y menores, bemoles de cuatro comas e intervalo 1/4 extraño al concepto de coma. La segunda emplea como base la escala pitagórica o de quintas, pero emplea hasta 8 tipos de sostenido y bemol, para configurar las escalas de los modos turcos. Estas notaciones aparecen en el tema 6.

Hemos preferido nuestra notación por encontrarla a la vez más sencilla e intuitiva. En la medida de la calidad de un temperamento, tema 3, se muestra la asombrosa precisión de esta división para dar cuenta de las escalas tradicionales.

A.13.7.9. Composición de intervalos

─────────────────────────────

Llamamos Intervalo Compuesto de otros dos al intervalo que separa las notas o tonos extremos cuando la superior de uno es la inferior del otro. La yuxtaposición de dos intervalos para formar uno solo consiste pues en hacer coincidir la ultima nota del primero con la primera del segundo, y tomar las dos extremas como nuevo intervalo. Por ejemplo, DO‑RE (+) RE‑MI (=) DO‑MI.

f1 f2 f3

├─────────────┼────────────┤

I1 I2

do re mi

y expresamos esa composición diciendo que I3 = I1 (+) I2, siendo este (+) un símbolo de unión. Numericamente ello se corresponde con el producto de las relaciones de frecuencias en vibraciones por segundo, o las de longitudes de cuerda; o bien con la suma de las medidas en cents. así tenemos:

NOTA (DO‑RE) (+) (RE‑MI) (=) (DO‑MI)

HERCIOS (100,112) (+) (112,125) (=) (100,125)

tono grande (+) pequeño (=) tercera mayor

INTERVALOS T (+) t (=) TM

9 10 10 5

QUEBRADOS ─── x ─── = ─── = ──

8 9 8 4

FRACCIONES 1.125 x 1.111 = 1.250

CENTS 204 + 182 = 386

Correlativamente, obtener el intervalo 'diferencia' de otros dos consiste en hallar otro intervalo que 'compuesto con el 'sustraendo' nos reconstruya el original. O sea, si contamos con una tercera mayor 5/4 y le 'restamos' el tono grande 9/8:

NOTA (DO‑MI) (‑) (DO‑RE) (=) (RE‑MI)

HERCIOS (100,125) (‑) (100,112) (=) (112,125)

tercera mayor (‑) tono grande(=) tono pequeño

INTERVALOS TM (‑) T (=) t

5 9 10

QUEBRADOS ─── / ─── = ──

4 8 9

FRACCIONES 1.250 / 1.125 = 1.111

CENTS 386 ‑ 204 = 182

A.13.7.10. División y Descomposición de intervalos

────────────────────────────────────────────

La división de un intervalo en otros dos, consistira en buscar una nota intermedia entre las que lo componen: DO‑MI ‑‑) DO‑re + re‑MI. Así que diremos que descomponer dos intervalos es encontrar un tono intermedio que crea dos donde había uno. Por ejemplo:

(300,100) = (200,100) + (300,200).

Algébricamente se trata de encontrar un número, intermedio entre numerador y denominador, con el que se forman dos nuevas fracciones mayores que la unidad, como indica el ejemplo siguiente. En cents, descomponer la medida en dos sumandos cualesquiera.

TM ‑‑) T + T

5 10 10 (9)

‑‑‑ = ‑‑‑ = ‑‑‑ x ‑‑‑

4 8 (9) 8

386 = 204 + 182.

Esta regla de división de intervalos la ofrecían ya los griegos antes de Cristo, y la recoge también Avicena, en el siglo XI. Veremos más ejemplos de división del tetracordio en el tema siguiente.

A.13.8. Bibliografía.

───────────────────

BENADE,A.H. Fundamentals of musical Acoustics. Oxford N.York,1976

DomCARDINE. Semiología Gregoriana Abadia de Silos, 198.

CHAMBERLIN,H. musical Applications of Microprocesso Hayden N.Jers.1980

DANIELOU,A. Traité de Musicologie Comparée. Hermann Paris, 1959

ERLANGER,R.D' La Musique Arabe. Vol.1‑6

Geuthner Paris 49‑64

GEVAERT,F.A. Histoire&Théorie d.l.Musique d.l'Antiquité

G.Olms Hildes 1965

GUETTAT, M. La Musique Clasíque du Maghreb

Sindbad Paris, 1980

HABA,A. Nuevo Tratado de Armonía

R.musical Madrid,1979

JARGY,Simon La Musique Arabe (Que sais je?)

P.U.F. Paris, 1971

LACHMANN,R. Música de Oriente.

Labor Barcel.1931

LEON TELLO,F. Estudios de Historia de la Teoría musical

C.S.I.C. Madrid.1962

MALM, W.P. Culturas Mus.Pacifico,Cercano Oriente&asía

Alianza Madrid 1985

REINHART,K&U. Turquie. Les Traditions musicales.

Buchet/Ch.Paris, 1969

SACHS,K. La Música en la Antiguedad

Labor Barcel.1934

SACHS,K. Musicología Comparada

Eudeba B.Aires1966

Sánchez,F.J. La Música Culta Arabe Oriental.

Coop.Univ.Madrid,1985

SCHÖNBERG,A. Tratado de Armonía

R.musical Madrid,1979

SCHÖNBERG,A. Funciones Estructurales de lsa Armonía

Labor Madrid,1990

STRANGEWAYS.F The Music of Hindostan

Orie.Rep. Delhi 1975

TOUMA,H.H. La Musique Arabe

Buch/Chat.Paris, 1977

SCHAEFFER,P. Tratado de los objetos musicales

Alianza Mús. Madrid,1988

─────────────────────────────────────────────────────────────────

E D U C A C I O N M U S I C A L. T E M A A . 1 4

T O C A R M U S I C A

─────────────────────────────────────────────────────────────────

INTRODUCCION

Se tratan algunos aspectos prácticos para elegir las obras a tocar en el Aula de Músicas, de acuerdo con las posibilidades que ofrece en el grupo.

INDICE

A.17.1. Elección de género.

A.17.2. Elección de obra.

A.17.3. Reparto de instrumentos y funciones.

A.17.4. Estudio y Ensayos.

A.17.5. Presentación pública.

A.17.6. Apoyos técnicos.

A.17.7. Bibliografía.

A.17.1. Elección de género.

─────────────────────────────────

Ante el maestro de música se abre un inmenso abanico, de posibilidades: ) qué música hacer ?. Recordemos para orientarnos todo lo dicho hasta ahora, sobre curriculum, audición, percepción, instrumentos, canto, danza, ...

Como género de música disponemos de toda la música, o las músicas: vocal, instrumental, moderna, antigua, folklórica, culta, nacional, extranjera...

Intentemos precisar: disponemos como datos del problema de:

1. Una clase formada por alumnos de una cierta edad, formación musical, idiosincrasía.

2. Un profesor dotado a su vez de esas mismas características.

3, Un aula dotada de determinados instrumentos y materiales.

Con estos elementos dados las posibilidades se reducen y sepuede concretar.

Que los niños tienen seis años y una nula formación previa: se incide sobre obras rítmicas, modales, instrumentos de afinación fija ( de láminas) y percusión. Timbres ricos, canción, siempre canción: infantil (pero no ñoña) o mejor popular.

Que se trata de alumnos de 12 años con una experiencia de tres o cuatro en clase de música: puede montarse un ballet, con coro, orquesta de flautas, láminas, percusión diversificada y si es posible, algun violín y píano. Todo con obra armónica y reparto orquestal.

Posibilidades: Jazz, Clásica, Popular‑Folklórica, etc. Dado el ambiente intrusivo que tiene el Rock y similares, no parece necesario incidir el la escuela sobre lo mismo, sino conpensar otros géneros menos habituales. Otra cosa es que algunos alumnos deseen hacia el final de la etapa primaria, comenzar a montar un conjunto de este tipo: que duda cabe de que aprenderán y trabajarán; es una iniciativa a favorecer, que aumenta en definitiva la actividad escolar musical.

A.17.2. Elección de obra.

────────────────────────

La obra se adaptará al género o tipo acorde con lo dicho antes.) Y la obra ?.

La obra debe tener corazón: debe llegar a los participantes y tocar su emoción, sin la cual, decíamos, no puede haber música.

Debe ser de calidad, es decir con valores formativos, para la clase, introduciendo elemntos nuevos en la enseñanza, sea en tímbrica, rítmica, melodía o armonía. Porque es importante la sensación de Progreso, de Logro. En todo aprendizaje es importante el mirar atrás y comprobar que se ha recorrido un camino, y que cada esfuerza o logro individuales son una etapa de un proceso más largo.

El nivel de dificultad admisible vendrá dado por el nivel de la clase. No hay que olvidar que en todad obra hay partes más complejas y otras menos, de modo que no hay porqué exigir que todos los alumnos dominen todas las dificultades: a cada uno según su capacidad.

A.17.3. Reparto de instrumentos y funciones.

───────────────────────────────────────

Ese reparto de funciones puede entrar en conflicto con un desarrollo equivalente deseable para todos los alumnos: pero no hay duda de que siempre se producirán diferencias naturales o aprendidas con lo que el nivel será desigual: corresponde al maestro adaptar la obra a las posibilidades que se encuentra. En concreto habrá porbablemente algunos alumnos que han empezado una enseñanza musical paralela y más especializada. Creemos que es preferible utilizar esos conocimientos que imponerles a esos alumnos una ejecución muy por debajo de sus posibilidades.

De todas maneras el resultado final depende del esfuerzo colectivo, y a nadie se le ocurriría pensar que el mérito de una obra se debe sólo a unos pocos. Todos colaboran de acuerdo con su situación, y las felicitaciones en caso de éxito serán para todos.

Por otra parte, aquellos que saben más pueden ayudar a los otros, con lo que todos están cumpliendo una función.

Así, se repartirán los instrumentos según las posibilidades de los participantes; en general se formarán varias secciones, por ejemplo, Rítmica, melódica, Armónica, Coros, y Cuerpo de Baile.

Cuanto más sencilla es la obra, menos secciones habrá, y , dentro de cada una, menos diferencias o papeles. En su simplicidad, la canción es una muica muy completa, que incluye una Voz o melodía, un Instruemnto, modal o armónico, y un Instrumento Percusivo, que marca acentos. Esta simple estructura puede multiplicarse sin complicarla, con un Coro monofónico, un Grupo Modal‑Armónico y un grupo Rítmico.

La diversificación puede realizarse repartiendo paepes dentro del grupo: ello exige ya conocimientos más extensos por parte de todos (incluído el profesor). Varias voces simultáneas precisan conocimientos de Armonía, varios Instrumentos diferentes, Instrumentación y Tímbrica.

Como criterio global, instruemntos grandes y graves tocan partes más sencillas y más básicas: bajos armónicos, pedales, acentos. Instrumentos pequeños y agudos, partes más complicadas y ágiles, adornos, frases de respuesta, etc. Y esto tanto en melodía y armonía como en ritmica, que lleva su propia proporción entre bajos y agudos.

La atribución de instrumentos a voces es delicada: es conveniente un coinocimiento empírico o estudiado ( combinación de espectros ) para combinar adecuadamente esos instrumentos. En general se trata, bien de conseguir lo que podemos llamar superinstrumentos, como la sección de primeros violines al unísono, saxo y trompeta, bajo y piano; bien de contrastar e individualizar, con lo que de combinarán instrumentos poco afines en timbre y tesitura: por ejemplo violín y piano, flauta y batería.

Estas ideas hay que realizarlas no lo olvidemos con el instrumental a nuestra disposición: flautas de pico, xilofones, panderos, rítmica pequeña, palmas, eventualmente flautas traveseras, pianos, violines etc.

Todo lo anterior se refiere a obras que monta el grupo: si existe una partitura con todo preparado y anotado, no hay más que seguir las instrucciones, aparentemente. Pero claro, sin un conocimiento de la materia, la ejecución será probablemente a ciegas. Además, debido a esa limitación instrumental, deberán probablente realizarse adaptaciones, versiones y sustituciones instrumentales: incluso habrá que meterse a retocar la obra, a simplificarla a veces; más argumentos para una buena formación musical del maestro.

Aparte del papel organizador que estamos comentando, el maestro puede, quizá debe, realizar una función también instrumental; bien completando un instrumento allí donde haga falta (papel de comodín, para el que hace falta versatilidad); bien para tomar una voz e instrumento para sí, generalemente una básica ( percusión central, armonía, etc), preferiblemente a solista.

A.17.4. Estudio y Ensayos.

─────────────────────────────────

El estudio musical será de dos tipos; el aprendizaje del instruemento, con partes colectivas y partes individuales; por otra parte el aprendizaje de una parte de la pieza colectiva.

También este preparación será individual al principio, colectiva después; incluso puede ser siempre colectiva si no hay dificultades especiales.

El conocimento de la lectura musical determinará además el tipo de ensayo: si no se tiene, se aprenderá colectivamente, en grupos pequeños coordinados por los alumnos mejor preparados, o los que simplemente saben la pieza. Incluso los que saben leer partituras sentirán mejor la pieza al oirla y aprenderla en grupo.

Se ensayará entonces por secciones, cuidando la compatibilidad mutua (afinación, tempo, ritmo, intervalica mútua). Después pueden combinarse las distintas secciones, cuando estas están razonablemente preparadas.

A.17.5. Presentación pública.

─────────────────────────────────

Una manera excelente de aunar interés y trabajo, es montar una o varias piezas para un recital o fiesta determinados. Esto proporciona responsabilidad a todos los participantes (sobre todo al sufrido profesor) y motiva a todos para un trabajo sostenido e interesante: quieren quedar bien.

La presentación pública acostumbra además a todos al enfrentamento con el público situación psicológicamente difícil que conviene pasar.

Dependiendo del interés y calidad de obra y grupo, puede pensarse también en recitales en otros centros culturales, colegios, fiestas privadas, concursos, etcc.

A.17.6. Apoyos técnicos.

────────────────────────

Es muy conveniente disponer de medios y conocimeintos técnicos que ayudan a la consecución de buena música: por supuesto buenos instruementos y accesorios, compo cuerdas, resinas, gamuzas, cajas.

Para afinar conviene utilizar diapasones acústicos: los afinadores electrónicos sólo son buenos para proporcionar la referencia; pero si se usan para afinar diferentes notas, como cuerdas de un instrumento o voces de un coro, se rompen las consonancias naturales que son las que han de oirse y se sustituyen por afinaciones calculadas mediante criterios simplistas y no musicales: el instruemnto no quedará afinado, sobre todo para instrumentos muy alejados del tesitura media (léase A.18.3.4).

Es muy útil un Cassette, grabador reproductor. Permite multitud de funciones, como aprender la obra mediante escucha repetida, transcripción de una obra grabada, grabación de una ejecuciuón para percibir y corregir defectos, ambientar la clase en períodos de relajación, etc.

La reproducción puede provenir del propio cassete, con ausencia de graves, o mejorarse con un equipo de audio (uno casero puede ser excelente) provisto de reproductor de discos, amplificador, cajas de altavoces (bafles). Es muy útil una pequeña mesa de mezclas de 6 u 8 entradas, que permiten combinar fuentes diversas, como cassette, micrófonos e instruemntos electrónicos si los hay (véanse A.18.3.4 y A.13.2 a este respecto).

Una cámara‑reproductora de video y un televisor añadirán la dimensión visual a la sonora, esencial en montajes de bailes y teatros musicales. Su utilidad en similar a la del cassete, ya comentada.

La iluminación también es importante, en sí misma y para la toma de video. En la ejecución pública es muy importante iluminar el lugar de ejecución (escenario o un rincón simplemente) y ensombrecer el respo focaliza la atención del auditorio en el acontecer sonoro y visual: se siente que 'lo importante' ocurre en el lugar iluminado, Si hay además focos de colores, pueden crearse diferentes atmósferas que ayudan a la fantasía; una luz azul puede convenir a un música nocturna y lenta; rojos, azules y amarillos dan un corido jubuloso que puede convenir auna escena de ballet rápida y dinámica.

A.17.7. Bibliografía.

───────────────────

SCHOCH,R. Educación musical en la Escuela. Kapelusz, B.Aires,1958

SWANWICK,K. Música, pensamiento y educación. M.Ed.Cien. Madrid,1991

WILLEMS, Edgar. Educación musical.Guía Didáctica para el Maestro. Ricordi, B.Aires,1966.

MARTHENOT Método Marthenot. Silfeo y Desarrollo musical. Ricordi, B.Aires,1979

VIVANCO,P. Exploremos el Sonido. Ricordi, B.Aires,1986

PERIS, J. Música para los Niños. Doncel. Madrid, 1965.

SANUY,M & González,I. Orff‑Sculwerk. Música para Niños. Un. musical. Madrid.1969.

GARCIA & LAGO La Innovación en la Educación Artística. UNED. Madrid, sin año.

SANDOR.F (ed). La Educación musical en Hungría. R.musical, Madrid,1985

HEMSY,V. La educación musical del niño. Ricordi, B.Aires,1964

MARQUES,S. Musique et mouvement à l'école. Edisud, Aix en Provence, 1990

TOUMA,H.H. La Musique Arabe Buch/Chat.Paris, 1977

SCHAEFFER,P. Tratado de los objetos musicales. Alianza Mús. Madrid,1988

Vuelta al Principio Última actualización: Monday, 04 de March de 2013 Visitantes: