 |
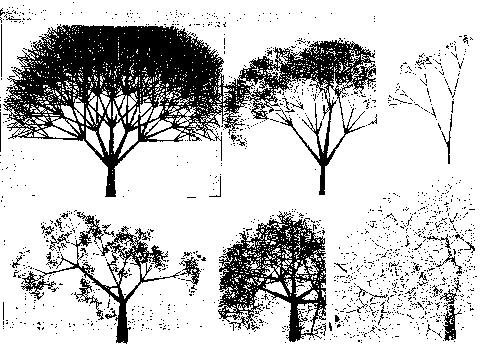
| Fig.1. Orden y desorden reflejados en estos árboles. |
Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
Una teoría numérica del ritmo aplicado a la Txalaparta
1. TEORÍA RÍTMICA
Proponiéndonos estudiar la música, o, más bien, aquellos aspectos de ella susceptibles de ser objetivados, habremos de reflexionar sobre lo que la Música es y sobre lo que la diferencia de otras artes u oficios. Su carácter sonoro la contrapone a las artes visuales, que quedan fuera de su ámbito –aunque sensaciones concomitantes como repetición, motivo, forma, etc., establecen puentes entre una y otras: pero esto es asunto más general cubierto por la sinestesia.
Circunscribiéndonos pues a lo sonoro, encontramos un grupo formado por la Palabra y la Música, y dentro de la primera, pero cercana a la segunda, la Poesía. Pero enseguida encontramos una radical diferencia, en cuanto a la expresión: mientras en la palabra se alude a conceptos o ideas del mundo externo (lo que constituye la Lengua) en la música se alude a –o mejor, se invocan– nociones no conceptuales. Podemos decir que en la palabra se cuentan cosas de fuera mientras que en la música se cuentan cosas de dentro. ¿Qué define pues a la música y la diferencia de esas compañeras, palabra y poesía, a las que dio quizá el ser, o de las que quizá proviene?
Si consideramos únicamente las características o rasgos sonoros que en palabra y música intervienen, observamos que ambas emplean como elementos relevantes el tono o altura del sonido, la intensidad de éste, su fragmentación en unidades de duraciones diferentes y el timbre de estos segmentos, formando una cadena o serie de segmentos cambiantes, al servicio de lo expresado.
No siendo diferentes los rasgos sonoros que caracterizan a palabra y música, ha de ser su uso quien lo hace. Y especialmente la introducción de la Medida es lo que separa la música de artes afines: en efecto es el Número, la medida de esos rasgos, lo que hace Música a la música, introduciendo Relaciones, Razones entre esas medidas: ello da la lugar a la Armonía en sentido general y también en el específicamente musical, como veremos. Pero es ya comprensible, de manera inmediata, que las relaciones sencillas entre duraciones de los elementos o unidades que llamamos notas o golpes, dan lugar a una regularidad de la que parten los sentimientos y las nociones de tempo, parte, compás, ritmo, conceptos ausentes en el habla natural, al menos con esa exactitud. Y, desde el punto de vista del tono, a diferencia del paso continuo por todas las frecuencias de su tesitura que efectúa la curva prosódica en el habla natural, en la música y canto la voz se detiene únicamente en un pequeño número de tonos y frecuencias (las notas de la escala): y son igualmente las relaciones sencillas entre estas frecuencias o tonos las que dan lugar a los intervalos obligados o preferentes (octava, 2:1; quinta, 3:2; cuarta, 4:3...) para construir escalas y acordes. Son estas regularidades las que resuenan dentro de nosotros, las que nos dicen cosas.
Es decir, que la Música, para devenir ella misma, renuncia a la infinita y continua variedad de duraciones y tonos, y se limita voluntariamente, para construir, en este universo limitado, formas más y más complejas. Y esto no es negado por la evolución de formas y estilos: estos y aquellas varían, pero sólo para ser sustituidos por otros nuevos.
¿Por qué esta autolimitación? Nuestra respuesta puede buscarse en la percepción o aparato unido a cada sentido a través del cual percibe. Es un hecho evidente que en los suceso sonoros atribuimos medidas subjetivas de los rasgos citados (de ahí su uso deliberado) y parece un hecho probado que sólo somos capaces de percibir directamente relaciones sencillas es decir de 1 a 2, de 2 a 3, más difícil de 5 a 4 (recuérdense los compases habituales). Así que en música empleamos relaciones que podemos percibir, y en la percepción de tales relaciones, y de alguna manera que todos (casi todos) sentimos pero que no podemos explicar (lo inefable), el espíritu se regocija.
Pero cuando hablamos de números en la percepción humana, debemos tener en cuenta aquellos mecanismos que nos describen cómo el oído-mente percibe ese número. Por ejemplo sabemos que las octavas son un poco más grandes que el intervalo de frecuencias representado por la proporción 2 a 1 (1200 cents.), principalmente en los rangos extremos (afinación extensa de las octavas extremas en el piano, escala mel). Por lo tanto una octava de proporción 2.01 puede ser apreciada como justa por el oído, en esos rangos, y todo análisis de intervalos debe tener en cuenta esta ‘distorsión’ que la percepción impone al número aritmético.
Así que la percepción influye en esas medidas, y en los números por lo tanto. Son siempre el 2 y el 3 quienes actúan, pero el 2 y 3 percibidos, que pueden no coincidir con la medida física. Número, vibración y oído, están pues inextricablemente unidos en la Música, o mejor, la hacen. Creemos pues que un acercamiento científico a la música debe utilizar métodos objetivos de medida: pero estos métodos deben incluir la función de transferencia (o filtro modificador) de la percepción humana.
Sin embargo, una vez establecido ese necesario universo numérico, en forma de ordenación que sustenta el edificio musical, necesita la Música para devenir arte, conservar o introducir una cierta libertad, traducida en modificaciones que, sin atentar, a la estabilidad de ese edificio, introduzcan variaciones o matices que despiertan la sorpresa, el interés y la expresividad de compositor e intérprete.
Podemos pues concluir que en la Música (y creemos que también en todas las demás artes) coexisten necesariamente, en conflicto permanente, esos dos conceptos, Orden y Libertad (o libertad y orden, según la ideología del momento); el orden la hace comprensible, y la libertad, amable e interesante. Pero sólo orden aburre, y libertad sola no expresa nada, y aburre igualmente; así pues, la Música es Prosodia (libertad expresiva) sobre Universales (número y orden).
El músico práctico, el intérprete, consciente de la extraordinaria complejidad del universo musical, tiende a desconfiar de la noción de número y otras nociones sencillas, considerándola simplista y, en todo caso, como una limitación a su libertad creadora, conquista del mundo occidental al que pertenece. Sin aludir al mundo oriental, más tradicional en su conjunto, el cual incide sobre todo en una fidelidad a unos principios (orden), hay que decir que ese músico occidental hace un uso continuo, sin saberlo a veces, de esa sencillez numérica que podría desdeñar. Cuando hace sonar una quinta justa, o cuando compone, toca o percibe un compás de 3 por 4 está haciendo números sin saberlo (define Leibnitz la Música como ‘un oculto ejercicio aritmético del alma, inconsciente de su contar’). El músico práctico sabe, pero no sabe que sabe, como no sabe la libélula de su volar, pero vuela. El objeto de la teoría es precisamente poner de manifiesto este saber empírico, en forma de conceptos.
Un ejemplo de orden necesario en la actividad más lúdica espontánea e 'inocente': cuando los niños juegan, siempre juegan a 'algo'; ese 'algo, es en definitiva un conjunto de reglas del juego, a las cuales los jugadores se someten voluntariamente para 'gozar más', ya que un juego sin reglas les aburriría enseguida. Cuando en el juego se dice que 'eso no vale, ¿no quiere esto decir que se han violado las reglas del juego colectivo?. Así pues, hasta los partidarios de una concepción lúdica de la música, deben, tomando ejemplo de sus maestros, los niños, admitir cierto grado de regulación y orden.
Véase otra ilustración de lo anterior. En los árboles de la figura, ejemplos de orden y número plasmados en forma, como hace la música, se observan extremos, tanto de orden, cuyo rigor ahoga la impresión estética, como de desorden, que desconcierta y ahoga también lo estético. Entre esos extremos hay un grupo de revolees entre los que el juicio y elección no es fácil, ya que afecta a lo social, histórico e individual; se siente sin embargo que es en ese grupo intermedio donde coexisten equilibrada y armónicamente orden y desorden, número y su violación: véase la figura 1 y opínese sobre ello.
 |
| Fig.1. Orden y desorden reflejados en estos árboles. |
1.2 Ritmo.
Concebimos el Ritmo con un patrón repetido casi igual, a intervalos casi iguales. En lo sonoro, este patrón es un conjunto de sucesos (notas, golpes). El carácter de ‘casi igual’, es importante: con tal de que haya semejanza, semejanza perceptiva entre las ejecuciones repetidas del patrón o motivo, hay repetición, retorno perceptivo, lo que mantiene la continuidad sonora; de modo que hay sucesos aislados, discretos, pero ligados en un todo (el ritmo) que permanece. Como decía un místico musulmán, el ritmo es la quietud dentro del movimiento.
Todo ritmo se basa en la coexistencia de dos frecuencias o velocidades de repetición: la del motivo o patrón, que corresponde frecuentemente al compás occidental, y la de un entramado o bastidor compuesto por intervalos de duración mínima –puntos temporales. Esta duración era conocida por los antiguos como chronos protos (CP), tiempo primo o primero, el cual modernamente corresponde a la duración del menor golpe independiente que aparece en una pieza u obra musical (decimos independiente porque duraciones menores pueden realmente aparecer como adornos, mordentes, trinos, etc., sin que su duración sea considerada, o sea, sólo aparecen como apéndice de otra nota de la cual toma su tiempo, se nutre, podemos decir).
Pero el pulsar interno de la música, el contar del intérprete, suele también emplear la parte, una organización interna de los CP del compás (2 o 3 de ellos). El tempo corresponde aquí a la frecuencia de repetición de esas partes, creando pues una categoría, intermedia entre las anteriores (compás y frecuencia del tiempo primo o pulso). De modo que en un 9 por 8 –realizado en tres partes iguales–, a 60 negras con puntillo por minuto, el compás se repite cada 3 segundos, la parte cada 1, y la subparte o tiempo primo, cada tercio de segundo (la corchea); esto en caso de que no aparezcan figuras más breves que la corchea, en cuyo caso la subdivisión sería mayor, de 9 por compás. Igualmente un 9 por 8 considerado como 4+5, caso corriente en las músicas de Oriente Medio, precisa un pulso o tempo de 9 CP por compás. En adelante sólo consideraremos partes sin subdividir, con lo que coincidirán parte y CP.
Recordamos aquí estos conocidos conceptos porque, acudiendo la notación habitual o cualquier otra que plasme esos dos elementos básicos, compás y CP (tiempo primo), tratamos de investigar si se aplican o no a al toque de txalaparta, lo que en un principio no puede ni afirmarse ni negarse. Ya veremos como ambas respuestas son ciertas, o ambas inciertas: el toque de txalaparta tradicional se encuentra entre el Orden y el Desorden.
1.3. Introducción a una teoría rítmica
En la zona del Egeo, Grecia clásica primero, y teóricos perso-árabes después, existía una teoría rítmica junto con la melódica: ambas seguían pasos similares, con conceptos homólogos como Géneros melódicos y Rítmicos, se conocía entonces el paralelo entre Ritmo y Melodía; esta consciencia se perdió posteriormente en Occidente, complicándose extraordinariamente el edificio tonal mediante la Armonía, y simplificándose (¿empobreciéndose?) paralelamente la Rítmica, hasta casi no precisar ya de una teoría (casi toda se escribió en compases sencillos, como 4 por 4 o 3 por 4).
Una de las grandes corrientes de aquel pensamiento antiguo era la Pitagórica, centrada en la importancia del Número para la comprensión y el orden (Logos) del Universo en general, y del Universo sonoro en particular. Los intervalos musicales percibidos con precisión y con agrado (consonancias) eran y son intervalos con proporciones sencillas entre sus frecuencias de vibración, o, equivalentemente, entre cuerdas o tubos que emiten los tonos que componen el intervalo. Así, hay una relación estrecha entre la sencillez auditiva de la Octava y la sencillez numérica de la razón de frecuencias, 2 a 1. asimismo y con consonancia decreciente se encuentran la quinta (3:2), la cuarta (4:3), la tercera mayor (5:4), la menor (6:5), etc.
Paralelamente, está claro que los compases más sencillos son aquellos representados por números sencillos: casi todo el mundo admitirá que el compás más sencillo es el 2 por 4, siguiéndole en orden no tan claro o el 3 por 4 o el 4 por 4; el 6 por 8 resulta más sencillo que el 5 por 8, e incluso el 8 por 8 y quizá el 9 por 8; así, sucesivamente vemos como algunos números pequeños resultan perceptivamente más complicados que otros mayores.
Fácilmente se intuye que las relaciones de divisibilidad juegan aquí un importante papel: en efecto, 4 por 4 es ‘sencillo’ porque 4 se concibe como 2 veces 2, o sea, como 2 por 2. igualmente 6 se concibe como 3 veces 2 (3 por 4) o 2 veces 3 (6 por 8). De modo que :
Un compás es tanto más complejo cuanto mayor es su número de partes, y menor es su divisibilidad, o sea, cuando admite pocos divisores, y grandes
Esto en cuanto a la longitud del compás. Ahora bien, ¿que ocurre dentro del compás?. También resulta claro que algunas de sus partes son ordenadoras y tranquilizantes, mientras que otras crean tensión y/o desorden. La primera parte tras la barra de compás es naturalmente la más relajante, la que resuelve, la más, digámoslo ya, consonante, rítmicamente hablando. Con ella se acaban generalmente las piezas, así como en el dominio tonal se acaba en la tónica, consonante y relajante, tonalmente hablando.
Si nos fijamos en un compasivo, 4 por 4, se admitirá que la parte más relajante, después de la primera, es la tercera, que corresponde a la mitad del compás. De las dos partes restantes, se ve también que la segunda en más consonante que la cuarta, la más inestable, porque esta última preludia, anuncia irresistiblemente la primera del siguiente compás. es la anacrusa, de máxima tensión y disonancia. de modo que casi todo músico y oyente admitirán una ordenación de esas cuatro partes del compás de compasivo con arreglo a su consonancia similar a la que vemos en la figura 2, siendo las cifras, más que medidas, indicadoras de una jerarquía. La disonancia variará inversamente (haciendo que ambas sumen 5, por ejemplo). Similarmente encontraríamos otras jerarquías para otros compases, como los que encontramos en la fig.3, haciendo que consonancia y disonancia sumen respectivamente 3 y 9:
|
||
|
Fig. 2. Atribución empírica de una consonancia rítmica a cada golpe de un compás de compasillo. |
A falta de más información tomamos con consonancia y disonancia similares las partes 2, 4 y 6 del compás 8 por 4, aunque es de esperar que no lo sean exactamente en la práctica perceptiva.
Se va pues viendo cómo los números plasman, reflejan la experiencia musical de todos. Intentemos ahora encontrar una medida, siquiera aproximada, de esas consonancia y disonancia (Sonancia llamaremos en adelante a la cualidad que, positiva o negativamente, miden) de compases y golpes dentro del compás.
| 3 por 4 8 por 4: | Parte y CP Consonancia: Disonancia: Parte y CP Consonancia: Disonancia: | 1 2 3 3 2 1 1 2 3 1 2 3 4 5 6 7 8 8 2 4 2 6 2 2 1 1 7 5 7 3 7 7 8 |
| Fig. 3. Atribución empírica de una consonancia rítmica a cada golpe de los compases de 3 por 4 y 8 por 4. | ||
4 Sonancia rítmica
Como el tono, el ritmo implica repetición: y en esta repetición cuenta la duración del ciclo o período repetido, que se percibe como altura tonal, en el tono, o como velocidad del tempo, en el ritmo. Pero, dentro de un margen pequeño (por ejemplo de 0.5 a 5 segundos), cuenta mucho la duración relativa de dos o más períodos. Se trata de un cociente, relación o razón de dos períodos. Cuanto más sencilla sea esa relación, como se sabe, más sencilla es su percepción conjunta, mejor consuenan, conciertan ambas rítmicamente. Todo esto concierne al contrapunto, (contraposición simultánea de puntos o notas de diferente duración). Si se baten dos tempos de frecuencia diferentes, comenzando con un golpe común, volverán a coincidir dos golpes en un intervalo temporal igual al mínimo común múltiplo de sus períodos de repetición: si se baten dos tempos de períodos en relación 2 a 3, coinciden otra vez dos golpes cada tres períodos del primero, o dos del segundo, es decir con un período correspondiente a 6 unidades de las que usamos en los dos primeros, como muestra la figura 4. Si los períodos son 4 y 5, obtenemos un período de 20, ya difícil de seguir. En cambio si los períodos no son números primos entre si, 8 y 6, por ejemplo, el período compuesto es menor de lo que podría esperarse (no el producto sino el m.c.m.); en realidad se trata de dos períodos en relación sencilla de 3 a 4, con período compuesto de 12. Todo esto es obvio.
En el apéndice se presenta una introduc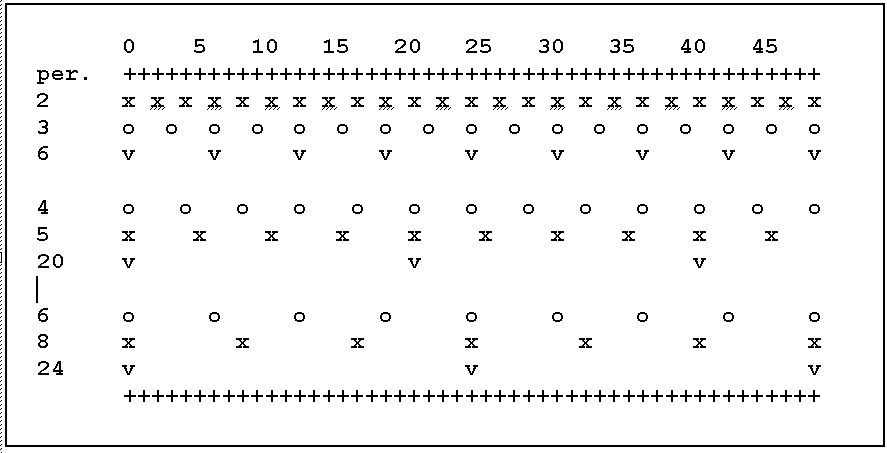 ción a las medida de
disonancia tonal para notas simultáneas, introducida por Euler, junto con
nuestra modificación. Puesto que tono y tempo son dos procesos idénticos
–repeticiones con períodos diferentes en proporción más o menos sencilla–,
nada nos impide aplicar esas teoría y medidas tonales a nuestro caso, el tempo.
Siempre que la proporción sea sencilla, lo que quiere decir racional (cociente
de enteros, y comprensible por la razón, nótese la simultaneidad o
bisemia numérico-pensante del concepto), podremos medir la disonancia rítmica
mutua de esos dos tempos; así lo hacemos en los párrafos siguientes.
ción a las medida de
disonancia tonal para notas simultáneas, introducida por Euler, junto con
nuestra modificación. Puesto que tono y tempo son dos procesos idénticos
–repeticiones con períodos diferentes en proporción más o menos sencilla–,
nada nos impide aplicar esas teoría y medidas tonales a nuestro caso, el tempo.
Siempre que la proporción sea sencilla, lo que quiere decir racional (cociente
de enteros, y comprensible por la razón, nótese la simultaneidad o
bisemia numérico-pensante del concepto), podremos medir la disonancia rítmica
mutua de esos dos tempos; así lo hacemos en los párrafos siguientes.
Dos tempos en proporción 1:1 tienen disonancia DE = 0, en proporción 3:2, DE = (2-1)+(3-2) =3, etc. es decir, los mismos valores que en el cuadro del apéndice. Nos encontramos pues con intervalos rítmicos esencialmente idénticos a los tonales, salvo el citado cambio de escala temporal. Podemos hablar así de octava, quinta, tercera rítmicas, en un bello paralelo ya conocido por los antiguos, cuando hablaban de géneros melódicos y rítmicos.
En este caso de relaciones sencillas, podemos llenar los espacios entre golpes de cada uno de los dos tempos compuestos con golpes más rápidos, tantos como sus períodos respectivos: de esta manera,
|
4
o...o...o...o...o...o...o...o...o...o...o...o...o 5 x....x....x....x....x....x....x....x....x....x... 20 v...................v...................v........ |
| Fig. 5. Compás de 20 por 8, obtenido con dos tempos con frecuencias en relación 5 y 4. |
los tempos citados se convierten en compases, siendo los golpes originales las partes principales del compás, y los golpes introducidos las restantes, como indica la figura 5: esas partes marcan, reflejan la racionalidad de los compases, su divisibilidad mutua. Podemos pues considerar que en la figura 5 aparece un compás de 20 por 8, agrupando las corcheas, bien en 4 grupos de 5, bien en cinco grupos de 4 (cinco blancas).
Si ahora elegimos un compás de cuatro partes, 4 por 4 por ejemplo, podemos considerar que, una vez establecida su repetitividad en nuestra conciencia (esperamos el primer golpe cada 4), la aparición de un golpe distinto del primero, crea una nueva frecuencia de repetición, que coexiste, se contrapone a la original del compás.
Por ejemplo, si se enfatiza la tercera parte, creamos un período de repetición de 6 partes contra las 4 del compás: tenemos dos períodos en razón 6 a 4, o sea de 3 a 2: se trata de una quinta rítmica cuya disonancia DE1 vimos que valía 3. A su vez las partes restantes conllevarían las siguientes disonancias: primera parte del compás, DE1(4:4) = 0, unísono rítmico; segunda parte, DE1(5:4) = 6, tercera mayor rítmica; tercera parte del compás, DE1(6:4) = 3, quinta justa rítmica; cuarta parte del compás, DE1(7:4) = 8, séptima natural rítmica. Las disonancias Euler se obtienen sumando una unidad a DE1 (véase el Apéndice).
| 4 por 4 PARTE y CP: 1 2 3 4 DEuler: 1 7 4 9 DE1: 0 6 3 8 DIS. INTUITIVA: 1 3 2 4 8 por 4 PARTE y CP: 1 2 3 4 5 6 7 8 DEuler: 1 8 7 14 4 16 9 10 DE1: 0 7 6 13 3 15 8 9 DIS. INTUITIVA: 1 8 3 8 2 8 4 8 |
| Fig.6. Comparación entre sonancias intuitivas y calculadas. |
La secuencia de disonancias encontradas es pues: 0, 6, 3, 8. Pero comparando esa lista con los valores deducidos directamente de la estimación intuitiva de la propia percepción rítmica (fig. 6), se encuentra que la ordenación, la jerarquía de esos valores (no los valores mismos, claro) es idéntica: primera parte poco disonante, tercera más, segunda más aún y cuarta, máxima disonancia. Nuestras magnitudes han venido pues a proporcionar una medida de nuestra percepción de disonancia, cuya exactitud resultaría difícil de comprobar, pero que indudablemente, tiene que ver, y mucho, con nuestro aparato de medida musical.
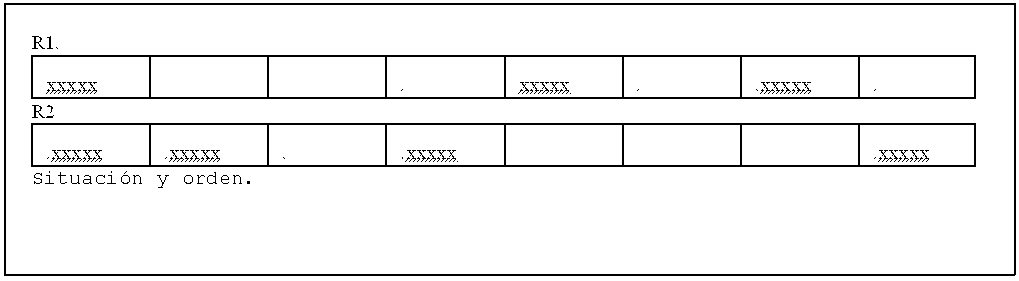 |
| Fig. 7. Dos ritmos de 8 partes y muy diferente disonancia. Cada golpe se numera con su situación dentro del compás, y con su orden rítmico, calculado contando su orden desde el compás anterior, empezando por 0. |
1.5 Sonancia de un ritmo
Una vez establecida la disonancia de cualquier parte de un compás, resulta fácil evaluar su efecto en un ritmo: aquellos compuestos de golpes disonantes serán ritmos más disonantes que los que usan golpes consonantes. Ambos pueden encontrarse en todas las culturas y épocas. Los primeros son tensos y excitantes, los segundos ordenadores. Compárense los dos ritmos de 8 partes en la fig.7 (xxxxx significa golpe en esa parte), y fácilmente se comprenderá, incluso visualmente, que el primero es mucho más ordenador (¿y aburrido?) que el segundo (claro está que cada ritmo tiene su aplicación dentro de las circunstancias de su uso, no se trata de establecer preferencias).
|
xxxxx |
. |
xxxxx |
. |
.xxxxx |
. |
|
.xxxxx |
.xxxxx |
. |
.xxxxx |
.xxxxx |
|
1 8 |
2 9 |
3 10 |
4 11 |
5 12 |
6 13 |
7 14 |
8 15 |
Consultando el párrafo A5, en el apéndice, calculamos la disonancia (de índice r = 1) para ambos ritmos, encontrando para el primero (véanse valores en fig.7) un valor para DE1 de CE1(8/8:12/8:14/8) = CE1(8×3×7) = 3+2+6 = 11; y para el segundo: CE1(8/8:9/8:11/8:15/8) = CE1(8×9×5×11) = 21, mucho mayor, como era de esperar.
Parece claro que, aún tomando estas medidas únicamente como indicativas u orientativas (a la espera de profundizar en su relación con la psique humana), nos resultan ya útiles para predecir los efectos de complejidad y disonancia de cada compás en particular, de cada golpe en ese compás, y de los ritmos realizados con golpes en ese compás.
1.6 Sonancia rítmica aproximada
Al medir los fenómenos que acaecen en la llamada realidad no se obtienen nunca valores exactos, bien porque no lo son las cantidades a medir, bien porque se cometen errores de medida, bien porque la medida misma es imprecisa en su naturaleza (piénsese en la medida de la frecuencia de una nota, por ejemplo, que prcisaría un tiempo infinito). Así que contamos siempre con valores inexactos, con lo que sus proporciones mutuas también serán inexactas y en general, no enteras: y sin embargo nuestra percepción nos certifica que la consonancia y los ritmos existen, porque los oímos; y además esas percepciones están ligados a los valores enteros cercanos a aquellos inexactos encontrados: comprendemos e interpretamos ritmos de 4, 5, 11 partes, pero no de 8.345 partes, no podemos concebirlos. Igualmente se comprende, se razona con quebrados, como ‘la tercera parte’, ‘tres cuartos’, 5 partes de 11, etc.
Está claro por lo tanto que el aparato perceptor realiza una operación de aproximación de aquellos valores, en proporción no entera, a otros en proporción entera; el aparato ajusta, ordena las frecuencias que oye de modo que formen un conjunto comprensible, sencillo, o sea, tan consonante como sea posible. Esta operación se realizará dentro de unos límites, ya que la experiencia nos muestra que a partir de una cierta divergencia o error, el intervalo deja de ser reconocible, pasando de intervalo desafinado a otro intervalo. Esa divergencia límite tiene gran importancia como vemos, pero es influida por muchas causas (costumbre, cultura, sistema musical, umbrales psicofísicos del oído, etc.) de modo que su estudio nos llevaría ahora lejos del tema que nos ocupa. En el apéndice puede verse el tratamiento matemático empleado para encontrar esos números sencillos que aproximan las duraciones que aparecen en un ritmo real.
En nuestro caso, una vez encontrados esos números sencillos, podemos considerarlos como duraciones de los intervalos entre golpes, medidas en CP. Además la comparación entre las diversas duraciones nos proporcionará el campás en el que aquellos sucesos sonoros se encuadran, caso posible pero no necesariamente cierto, ya que hay músicas y golpes sin compás definido. Conocidas esas posiciones dentro del compás, podremos estimar asimismo su disonancia rítmica mediante las fórmulas anteriores. En las secciones dedicadas a la txalaparta pondremos de manifiesto esas medidas y estimación de compás; y en el apéndice, sección A5, las sencillas técnicas matemáticas empleadas para realizar aquella aproximación. Pero ya puede comprenderse que se trata de encontrar una ‘vara de medir’, una unidad temporal, el CP, con la que todos los intervalos temporales entre golpes arrojen enteros, sean múltiplos (¡pequeños¡) de esa unidad.
De esta manera, hemos conseguido encontrar un criterio para evaluar las disonancias o tensiones de cualquier ritmo. Como prometimos, intentaremos aplicar tales nociones al toque de la txalaparta vasca.
2. APLICACIÓN AL TOQUE CLÁSICO de TXALAPARTA.
2.1. El toque clásico.
Pertrechados ya con nuestro criterio de disonancia rítmica podemos volver los ojos a nuestro instrumento y ver de aplicarlos a su toque. Se trata de encontrar el compás o compases del toque y después, el ritmo o ritmos que en él o ellos se encuadran. Podremos entonces evaluar sus propiedades sonantes y comprobar si los conceptos anteriores nos permiten describir, explicar psicológicamente lo que ocurre desde que se comienza a tocar a hasta que se acaba.
Vamos a examinar con algún detalle dos toques de txalapartaris zaharra pertenecientes a la zona que rodea Donostia-S.Sebastían, que abarca Lasarte, Hernani, Usúrbil, Astigarraga, etc. Centramos este estilo o manera en dos familias: los Zuaznabar de Lasarte y los Goikoetxea de Astigarraga; dos de los miembros de ésta última, Ramón Goigoetxea y Ion Urbieta, colaboran en el primer toque que estudiamos (que puede oirse en Beltran, 91). En adelante entiéndase ‘toque clásico’ cuando hablemos del ‘toque’, y limítense a aquél los comentarios y conclusiones a que se llegue, salvo cuando se diga lo contrario.
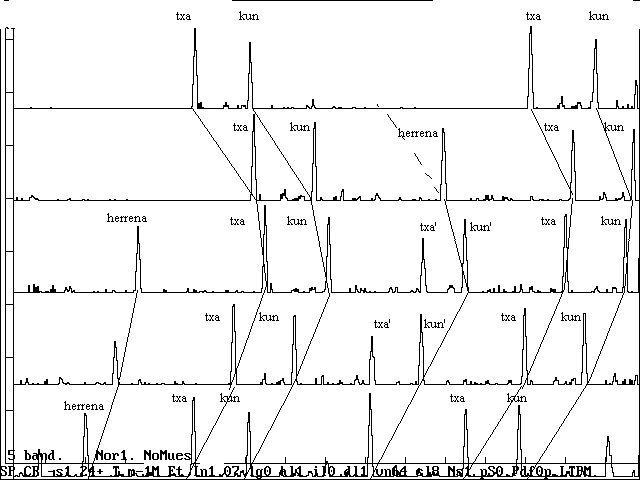 |
| Fig. 8. El principio de un toque clásico: etapa de establecimiento. Cada línea representa 1.82 seg. Los golpes aparecen como picos, y su separación indica el intervalo temporal. Nótense los txan (aquí llamados herrena) adelantados respecto al medio del intervalo kun-kun. En la fig.11 aparece el toque completo. |
2.2. Descripción del toque y de su carácter esencialmente binario
El toque de la txalaparta es dual, se realiza entre dos personas. Ni una, como ocurre con otros instrumentos y otras músicas (solo de piano), ni varios (como en la orquesta), salvo que estos varios se agrupen en dos papeles alternados para tocar la txalaparta. Esta carácter dual o binario del toque, tiene como consecuencia un carácter binario del compás o medida rítmica, ya que a cada uno le corresponde la mitad del tiempo. Además proporciona una alternancia entre ambos txalapartaris, pero claro está, con
 |
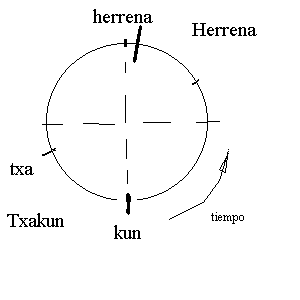 |
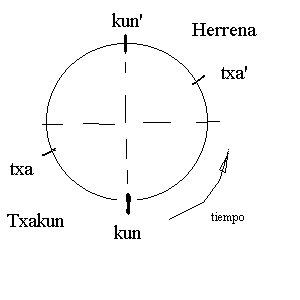
| Fig. 9. Otra vuelta de txalaparta: comienza y acaba en kun de txakun; txa'kun' de Herrena muerto o pasivo, con kun' en el medio. | Fig. 10. Una vuelta de txalaparta: comienza y acaba en kun de Txakun; txan de Herrena vivo, adelantado respecto al medio |
una función diferente.
El primero, conocido como Txakun o Tukutun (con mayúscula en lo que sigue) comienza golpeando con ambos palos, dos golpes seguidos, llamados también txakun (con minúscula en adelante). Espera un intervalo (previsto para su compañero) y vuelve a repetir ese par de golpes (fig.8). Tras unos pocos txakun de este tipo (en rigor, con dos bastaría) el otro txalapartari, llamado Herrena, coloca en un cierto momento sentido como ‘enmedio’ un sólo golpe, llamado txan (como antes, diferenciamos función y golpe con mayúscula y minúscula, respectivamente). Esto establece el principio del diálogo. creando la alternancia temporal que sirve de base al resto del toque.
En vueltas sucesivas, Herrena coloca más golpes txan,
o pares txa’kun’ (lo escribimos con apóstrofes para diferenciarlos
de los golpes similares de Txakun), creando nuevos patrones rítmicos;
pero lo hace de tal manera que va inestabilizando el compás inicial. Esto lo
realiza adelantando sutilmente sus intervenciones, txan o txa’kun’,
respecto al medio exacto del compás, situación sentida como muerta o estable
(fig.9). El adelantamiento, en cambio, dinamiza el tempo, creando una tensión
que intenta ser resuelta, anulada, por el Txakun, el cual intenta
asímilar los golpes adelantados del Herrena a un nuevo compás
, más
rápido (fig.10).
El proceso es sutil porque para ello aquellos golpes del Herrena deben ser incomprensibles para el antiguo compás, de ahí su poder dinamizador (un golpe decididamente fuera del medio citado, sería comprendido como una sugerencia de un nuevo patrón rítmico pero dentro del antiguo compás: se trata de un mensaje que tiene que ver más con el ritmo que con el tempo). En todo caso, Herrena coloca sus golpes en el espacio que va desde el kun del Txakun an medio del compás, ese es su territorio. Si se atrasara en lugar de dinamizar, ralentizaría el ritmo, con una sensación inadecuada. En la figura 9 se ilustra este delicado proceso que acabamos de describir.
El resto de este diálogo seguirá contraponiendo la regularidad de los golpes del Txakun con la inventiva y variación de los del Herrena; el toque, este diálogo, se hace entre los dos, pero con función diferente: Txakun mantiene equilibrios y recuerda referencias. Herrena, varia, sugiere, llena o no, creando motivos y patrones que cubren varias vueltas. Encontramos aquí la antigua dualidad orden-desorden, macho-hembra, ying-yang, payaso-augusto, noche-día, etc.
|
|
| Fig. 11. El toque clasíco completo (Goitcoetxea-Urbieta) cuyo principio aparecía en la fig.8. Cada línea representa 1.82 seg. y la duración total son 61 seg. Se marcan los kun de Txakun que señalan principio de vuelta o compás. |
En la figura 11, se representa el toque completo. Se pueden contar en él 128 vueltas, con una duración de 61 segundos, lo que da una duración media de aproximada de medio segundo por vuelta. Se han marcado manualmente todos los kun del Txakun, que corresponden a barras de compás (fig.13). Hacia la mitad se observa una zona de aspecto regular, lo que pone de manifiesto gráficamente la regularidad temporal del toque; la aceleración progresiva del tempo se ve reflejada en la forma de 'D' de las ondas aparentes. Incluso puede observarse como las ondas 1, 4 y 5, 8 y 9, 12 y 13, y 16, que corresponden a los txakun, son mucho más regulares que las intermedias, correspondientes a Herrena tocando txa’kun’; se observa así gráficamente cómo la regularidad de Txakun contrasta con la inventiva de Herrena. Orden y Desorden aparecen otra vez, reflejados en la figura 12.
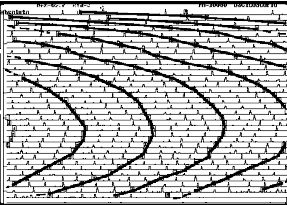 |
| Fig.12. Curvas de compás: orden y desorden. |
Puede ver un gráfico del primer toque utilizando la notación usada en Hernani, en la figura 12-B
 |
| Fig.12-B. El primer toque utilizando la notación usada en Hernani: raya arriba, ttxakun. raya abajo, herrena. |
2.3. Interpretación musical del toque: tempo, compás, ritmo.
Uno de los txalapartaris comienza con un par de golpes, llamados igual que el intérprete, txakun, onomatopeya clara del sonido (ver otra vez, la fig.8). Tras un intervalo repite la pareja, una o más veces. En ese instante acaba de crear el ciclo primario del toque (una vuelta lo llaman algunos), el que correspondería al compás y al tempo: en efecto, el intervalo entre parejas (patrón rítmico sencillo inicial) nos proporciona la duración del compás o vuelta, el intervalo entre los dos golpes de la pareja txa-kun la duración de una sola parte o CP (porque es la menor duración que aparece (recuérdese el párrafo 1.2, Ritmo) y la relación o razón entre esas dos duraciones nos indica auditivamente, cuantas veces la primera está contenida en la segunda: nos proporciona pues el número de partes del compás. A su vez, obtenemos el batido de las partes, que corresponde al tempo del toque.
| Vuelta de 5 0)))))))))))))))0 t k t’ k’ t k )2))2))))0))0))))2))2) 1 2 1 2 1 |
| Fig.13 Una vuelta típica de toque clásico: notaciones de la Escola de Hernani y la musical tradicional. Plicas arriba, Txakun. Plicas abajo, Herrena. Duraciones entre golpes y compás resultante. En vuelta 4 de primer toque (fig.8 y 11) |
¿Qué nos falta ahora? Sólo el principio del compás, elegir cuál es la primera parte; en principio ambos golpes en la pareja txakun son candidatos, debiéndose elegir entre un motivo anacrúsico, yámbico (del tipo ‘ta TÁ’), o trocáico (del tipo ‘TÁ ta’). El carácter algo más fuerte del segundo golpe parece ya indicarnos que la primera forma es la adecuada; pero ese énfasis no es siempre cierto; incluso la onomatopeya empleada, txakun, sugiere un segundo golpe prolongado e importante. Pero la función decisoria está reservada al segundo de los tocadores. al Herrena, precisamente cuando da el golpe único carcterístico: el txan, golpe único sentido ‘en el medio’ de dos txakun. Ese golpe se encuentra situado aproximadamente entre los dos kun según se veía en las figuras 8 y 11, marcándolos así como primeras partes del compás o vueltas que estamos estableciendo. Y se comprende que otro txa’kun’ del Herrena no serviría a este propósito, pues perpetuaría la duda entre motivo anacrúsico o no. Creemos pues haber encontrado el proceso perceptivo que ambos txalapartaris, en colaboración, usan para notificarse mutuamente y a los oyentes, el marco rítmico en que va a desarrollarse el toque. Y es interesante el hecho de que aunque la tradición del toque podría dispensar de este preámbulo, se conserva éste, necesario para oyentes nuevos. En la figura 13 se representa la vuelta así percibida, la notación empleada en la Eskola de Hernani, las duraciones encontradas, perceptivamente y según las técnicas aproximadas descritas más adelante y el compás que refleja todo lo anterior. Se alcanza así la primera fase, que podemos llamar de Establecimiento.
En vueltas sucesivas se repiten los txan del Herrena, o bien éste introduce txa’kun’ o calla en su zona temporal; esta simple alternancia de tres posibilidades, txan, txa’kun’ o ‘no’ (silencio), crea ya efectos interesantes, porque se perciben entonces grupos de vueltas en forma de frases rítmicas, del tipo mostrado en la fig.14. Herrena se comporta así como un vinculador de varios txakun en grupos de fisonomía variada. Los txa’kun’ del Herrena se colocan de modo que el kun’ coincida con el medio del compás: esto equipara ese kun’ con el txan, quedando el txa’kun’ como un txan precedido de otro golpe.
|
txakun-txa'kun'-txakun-txan -txakun-txa'kun'-txakun-no txakun-txa'kun'-txakun-txa'kun'-txakun-txa'kun'-txakun-no |
| Fig.14. Frases características formadas entre los dos txalapartaris de un toque clásico. |
Esta etapa podemos llamarla de Desarrollo. En ella se va acelerando el tempo, con oscilaciones que pueden atribuirse bien a efectos buscados, bien a errores humanos de variaciones hacen el toque vivo y cambiante, distinto del toque maquinal que ahora puede realizar cualquier sintetizador o secuenciador informático.
El tempo de acelera más y los txalapartaris sienten que se acerca el final: en un cierto crescendo de intensidad y expresividad, se preludia ese final, que se realiza efectivamente cuando Txakun varía por primera y última vez su toque, omitiendo el segundo golpe. Ese Txa final marca sin dudas que el toque ha acabado, lo que culmina la tercera etapa considerada, la de Cierre, y el Toque mismo.
2.4. Complejidad rítmica del toque
La observación de los gráficos anteriores muestra, mediante simples mediciones temporales que, en este toque clásico, se pasa desde un lento compás aproximado de 12, 11 o 10 por 8 al principio, hasta un rápido 8 por 8 aproximado al final (algunos txalapartis lo llaman lauko, de cuatro) o incluso compases aún más cortos. Como el proceso es gradual, quiere esto decir que se pasa por compases de medidas intermedias, lo que complica extraordinariamente la rítmica consiguiente. En efecto, si pasamos gradualmente del 12 al 11, deberemos pasan necesariamente en algún momento por 11.5 por 8, lo que equivale a un 23 por 16: ya ésto se siente como difícil de tocar y percibir; pero es que para pasar de 11 a 11.5 se pasará también por 11.25 (un 45 por 32); y así pasaremos también por 11.1 por 8 (correspondiente a ¡111 por 80!). No aseguraremos al llegar a estas conclusiones que los txalapartaris y su auditorio son conscientes, musicalmente conscientes, de estas enormidades. Más bien creemos que intérprete y oyentes simplifican esos compases, y saltan, o creen saltar entre compases mucho más simples. Pero no hay duda de que aquellas complejidades están ahí, y de que por lo tanto, algo complejo se percibe: ese algo entonces intriga, interesa, y así el toque está vivo.
| txa‑kun kun‑herr herr‑txa | kun‑kun Compás 121 614 736 6 : 8 140 620 761 5.43 : 8 127 284 281 694 5.45 : 8 131 284 278 694 5.3 : 8 108 115 147 505 3.76 : 8 |
| Fig. 15 Intervalos en miliseg. entre golpes y compases aproximados |
La comparación de duraciones entre golpes nos proporciona valores aproximados del compás, como se indica en la fig.15 Txakun comienza con un 6 por 8 aproximado, que rápidamente, con la entrada de Herrena, pasa a ser de 5.75 por 8, o sea, de un 23 por 32 aproximadamente. Algunos de los primeros compases, como el primero en la fig.16, proporciona un valor de 4.75:4 o sea, 19 por 16. Su escritura musical aproximada ofrece aspecto que le sigue más abajo, en el primer compás.
| t-k k-t’ t’-k’ k-t | k‑k comp 134 169 108 223 | 636 4.75:4 4 5 3 7 19 19:16 1916 q l q Å X Å X Å ¨ q l 134 108 115 147 | 505 3.76:4 8 6 7 9 15 30:32 |
| Fig. 16. Intervalos en milisegundos entre golpes. Compases resultantes tras aproximar mediante cociente de enteros |
El compás, medido como antes, arroja ya valores más cortos que el 4 por 4: en efecto, se obtienen valores de 3.8 o 3.7 por 4, correspondientes a 15:16, o 30:32, como se ve en la fig.16. En todo caso, no se detienen los txalapartaris en valores sencillos; de ahí el carácter sincopado, cojo del toque. De hecho el txalapartari viejo llama algo desdeñosamente de tren al toque regular, indicando quizá su falta de interés. Mediante las técnicas aproximadas descritas en el apéndice, encontramos automáticamente en qué proporción se encuentran los intervalos temporales txa-kun y kun-kun (en dos vueltas sucesivas). Encontraremos fracciones del tipo 1:4, 1:5, 1:6; o 2:9, 2:11, 2:13, etc.:, en general m:n; esto equivale a haber encontrado el compás aproximado: n por 4×m : en efecto, 1:5 equivale a 5 por 4, 2:11 equivale a compás 11 por 8, 3:10 equivale a 10 por 12, y así para otros. En la fig.17 se muestra este análisis efectuado sobre el principio del toque (fig.8). Se comprueba el paso de compás de 6:8 en la primera fila a 5:8 en la segunda, y 4.5:8 (9:16) en la tercera (quinta vuelta) y quinta (novena vuelta) filas. Estos resultados se alcanzan si no tomamos en cuenta el txa’ cuando existe, porque entonces el resultado sería más complejo. Repetimos, ¿son intérpretes y oyentes concientes de estas complejidades? ¿Oyen estos complejos compases o simplemente perciben situaciones rítmicamente inestables?. No podemos responder a ello, pero sería interesante hacer pruebas al respecto.
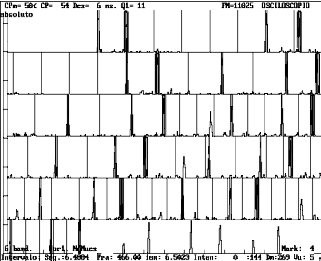 |
| Fig.17. Asimilación del principio del primer toque a compases medidos mediante tiempos primos. Paso de 6:4 (12:8) a 11:8 según la estimación de SETS30. |
2.5. Otro toque clásico.
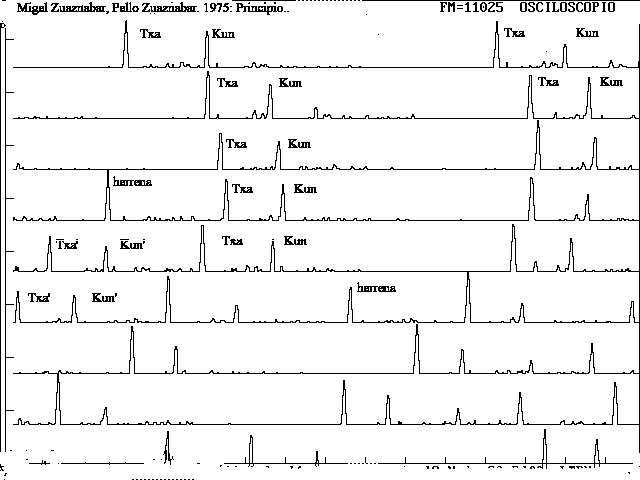
En el segundo toque considerado, interpretado por Mikel y Pello Zuaznabar en 1975, encontramos la disposición que se muestra en las figuras 18 y 19. El establecimiento es parecido, con varios grupos txakun y un primer txan (fig.18). La duración del compás va disminuyendo rápidamente, y se percibe ya una acortamiento (cerramiento) del espacio txa-kun, lo que parece mantener el compás más estable que en el primer toque (recuérdese que acortamiento del compás y cerramiento de txakun son efectos contradictorios).
|
| Fig. 18. El principio del segundo toque clásico: etapa de establecimiento |
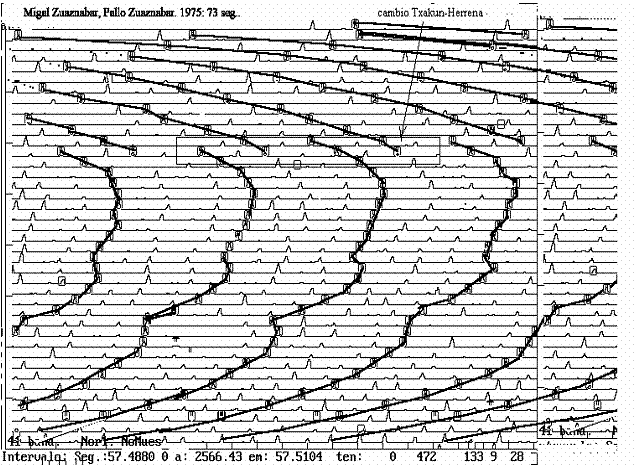
Se produce en este toque, no obstante, un hecho curioso, claramente visible en la fig. 19: los papeles de ambos txalapartaris cambian en la zona marcada, notándose este hecho acústicamente y gráficamente. En concreto, en el segundo 24, Txakun omite sus dos golpes, pasando entonces el txa’kun’ de Herrena a cumplir como txakun, lo que se consagra con un txan único golpeado por quien hasta ahora fur Txakun, pero que deviene Herrena en este corto proceso que acabamos de describir. La audición, por su parte, encuentra una zona en la que el compás parece disolverse, restableciéndose después. El gráfico muestra además, que el hecho se debe al cambio descrito, pasando Herrena a Txakun y viceversa, y asumiendo por lo tanto los papeles de orden y desorden que ambos conllevan.
|
| Fig. 19. El segundo toque completo, mostrando el intercambio de papeles o funciones entre los dos txalapartaris, marcada por el cuadro: nótese la ausencia de txa-kun en seg.24, junto a su esquina izquierda inferior.. |
Este cambio de función (debido quizá a una interferencia en lo musical del temperamento de uno de los músicos) parece ser excepcional, pero hemos descrito este toque tanto para mostrar los vicisitudes de un toque real, espontáneo, en directo, como para mostrar las posibilidades de estos gráficos para reflejar esas vicisitudes.
2.6. Visiones rítmicas del toque
El toque tradicional de la txalaparta puede así concebirse como un ritmo variable inserto en un compás de estructura decreciente (menor número de partes) y un tempo creciente. El decrecimiento del compás lo provoca principalmente el Herrena, adelantando su(s) golpe(s) respecto a la mitad del compás: ésto crea la tensión o desorden. El Txakun intenta restablecer el orden reduciendo la duración del compás, para llevar los golpes del Herrena a esa mitad; pero además, para no reducir en exceso el número de CP de ese compás, acorta también la duración del intervalo txa-kun. Así, uno u otro o los dos, van acortando el tiempo entre el par de golpes propios (txa y kun), lo que acorta el tiempo de la parte, y acelera de hecho el tempo de la pieza. Por lo tanto, en ésta célula del proceso se acelera tempo y acorta compás. Se ilustra este proceso en las fig.20 y 21.
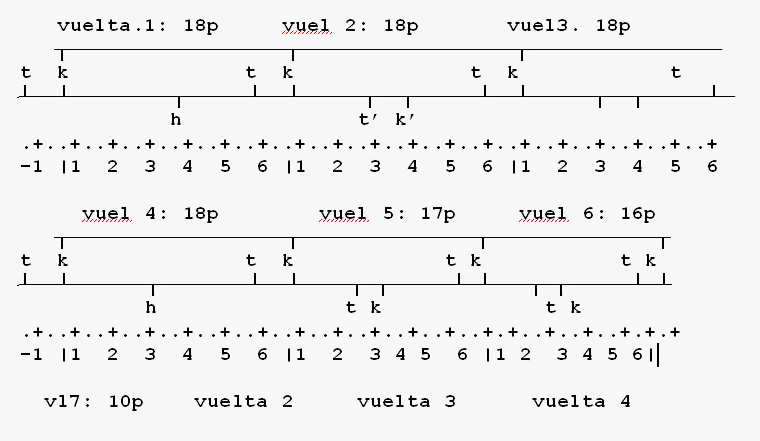 |
| Fig. 20. Ilustración del aceleramiento y cambio de compás en 3 etapas. Se pasa de un compás lento (parte dura 3 unidades) y largo (6:8) a rápido (parte dura 2 unidades) corto (5:4), pasando por compás rápido y largo (último de la fila central).. |
Este diálogo acalorado, apasionado, podemos decir, cesa cuando se alcanza el equilibrio o saturación, en el que uno o ambos talapartaris no quieren o no pueden llevar más allá este proceso tensión-resolución, por agotamiento psicológico (emocional, nervioso), físico (fatiga), o mixto (deja de concebirse comprenderse el patrón cambiante formado por ambos músicos, no se llega a insertar correctamente los golpes entre los del otro). En todo caso, el Txakun cerrará normalmente el toque con un sólo golpe fuerte, cuya excepcionalidad (un golpe en lugar de los dos habituales) y su situación (es un txa) le caracteriza como cierre. Así pues, en el toque de txalaparta, más que tocar un ritmo entre dos músicos, se hace y se deshace un ritmo de manera continuada, un una tela de Penélope siempre cambiante; si hay un ritmo, es un ritmo fugitivo que cambia cuando empezamos a percibirlo. Más que una colaboración es una lucha (con reglas) entre el Orden y el Desorden.
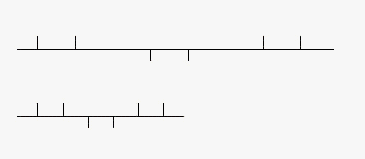 |
| Fig. 21. Ilustración del comienzo y fin del toque: de compás lento y largo (6 por 4) a rápido y corto (4 por 4). |
Si llevamos todo esto a un entorno náutico, lo que es un ritmo colectivo --como las tamborradas, como el toque de batería--, al remo del equipo de una trainera, lo es el toque de txalaparta al siguiente juego sobre una barca: uno de los pasajeros rompe la estabilidad arrancando un trozo de su lado; el otro restablece el equilibrio arrancando a su vez un trozo del suyo, y así sucesivamente; siempre hay barca, pero no la misma que empezó el viaje --ni son los mismos los viajeros, ya que han pasado por una fuerte experiencia. Otra imagen: entre dos personas se trasporta un tablón. Uno de ellos acorta su extremo (para aliviar su parte del peso). El otro siente el desequilibrio, y lo restablece cortando un trozo del suyo: el tablón queda más corto, es más ligero, y ambos caminan pues más rápido. Enseguida se repite el ciclo, ambos transportistas se encuentran más cerca, andando más rápido, y así sucesivamente, hasta que no pueden cortar porque se quedan sin tablón, o porque corren demasiado aprisa y temen caer. En ese momento cesa el viaje.
2.7. Otros toques
En las páginas anteriores se ha estudiado un toque tradicional, y se han obtenido conclusiones sobre lo que en él ocurre. ¿Quiere esto decir que así debe tocarse la txalaparta?. De ninguna manera. El estudio saca enseñanzas de aquel toque pero no intenta sentar cátedra no agotar las posibilidades. Una visita a la anual Txalaparta Festa de Hernani demuestra la inventiva, originalidad y posibilidades diferentes que el instrumento ofrece para quienen lo golpean (o tañen, que así puede calificarse a algunos toques). Pero pensamos que en ese toque tradicional hay un elemento que hace de la txalaparta un caso aparte: la citada pugna entre orden y desorden rítmicos representados por ambos txalapartaris. Ésto constituye, en nuestra opinión, una valiosa característica del toque clásico; y pensamos que incorporarla a los nuevos toques, junto a sus nuevas y mayores libertades rítmicas y tímbricas, sería una bella y sabia manera de enlazar lo nuevo con lo viejo, la Modernidad con la Tradición
2.8. Procedimientos de medida
Las figuras 8, 11, 12, 17, 18 y 19 , que representan los golpes de una manera simple, han sido realizados mediante el paquete SETS3 --subpaquete 30--, desarrollado en nuestro laboratorio (Fernández y otros, 90). La señal digital contenida en el CD citado se convirtió en una señal en el entorno Windows para PC-AT, con nombre >txala2.wav=, señal que fue leída y procesada por SETS30. Este proceso consistió en diferenciar (>derivar=) la señal, lo que atenúa las bajas frecuencias y destaca las altas, más importantes durante el golpe mismo, el cual aparece así como un pico claramente visible. Las distancias entre picos, correspondientes a intervalos entre golpes son medidos por el programa e impresos en forma de tabla. Y se hallan los CP aproximados que corresponden a los intervalos entre esos picos mediante el proceso descrito en el apéndice. Se ha dispuesto así tanto de la versión sonora del toque, como de varias representaciones gráficas y de medidas de duraciones sobre ellas, lo que permitió cotejar simultáneamente impresiones audibles, visuales y numéricas. Se han consultado asimismo gráficos similares preparados por Andrés Doñate (Joaldia), a quien agradecemos aquí su desinteresada colaboración.
Por otra parte, las conclusiones rítmicas deducidas en este artículo se han probado mediante el programa TecnoTxalaparta, desarrollado igualmente en nuestro laboratorio. El programa es capaz de tocar y oir simultáneamente con un ser humano, estimando el ritmo que éste va imponiéndo al toque y adaptándose a él, pudiendo actuar la máquina como Txakun o como Herrena. Se dispone así de dos paquetes informáticos que pueden contribuir eficazmente al estudio y conocimiento del toque real de la txalaparta, junto con otras importantes aplicaciones en análisis melódico y rítmico de música y palabra.
3. CONCLUSIONES
En las páginas anteriores se ha propuesto una aplicación de las teorías numéricas de la consonancia tonal al ritmo de duraciones, mostrando la relación de la psique con el número, y llegando incluso a medir esas consonancias. En un apéndice, la teoría de la consonancia de Euler se expone, se generaliza, bajo el nombre Disonancia Esencial, y se aplica para medir la sonancia de ritmos considerándolos como una combinación de golpes de complejidad varia.
También hemos visto cómo ese modelo teórico del ritmo, basado en conceptos-perceptos de orden y desorden que toman forma y medida mediante el número, es eficaz, quizá indispensable, para concebir intelectual y musicalmente lo que ocurre en un toque de txalaparta. Por otro lado se ha mostrado asimismo la utilidad de los métodos de tratamiento numérico y gráfico de la señal para mostrar, para poner de manifiesto aquellos conceptos de orden y número, para medir y para encontrar los valores o figuras musicales a que dan lugar.
Los métodos anteriores, teóricos y prácticos, pueden (y creemos que deben) extenderse, primero a los toques de txalaparta no tradicionales, para compararlos con los aquí estudiados; segundo, a otros instrumentos vascos, ritmos y melódicos --ya que ambos hacen ritmo al tocar--; tercero, a otras rítmicas, instrumentos y culturas, en particular a aquellas que, como algunas africanas (bereber, gnaua) y orientales (japonesa) aplican, como la txalaparta vasca, el acortamiento progresivo del compás; y, por último a otros fenómenos similares al ritmo musical, como es el habla artística de la poesía y teatro. Incluso al terreno visual pueden extenderse estas vivencias y conceptos esenciales que conocemos como Ritmo.
En absoluto creemos haber agotado este importante tema de la Disonancia Rítmica: la complejidad adicional del patrón tímbrico, fundido con el de duraciones; la repercusión del tempo en la complejidad total --una velocidad muy lenta o muy rápida hace todo más difícil de percibir--; intensidad, esencial para dar vida, expresión a los ritmos ejecutados; --ritmopoeia--; articulación, o enlaces variables entre golpes contiguos; distinción entre golpes importantes y de relleno en un ritmo dado. Todos esos aspectos añaden complejidad, interés, belleza al sistema total, mientras que nosotros hemos considerado uno sólo de los aspectos; ahora bien, es el más importante, ya que las propiedades de periodicidad del ciclo y parte de lss sensaciones de retorno dependen de él.
Sin embargo, esperamos haber traído una nueva visión a este olvidado dominio del ritmo, permitiendo progresos posteriores. En este limitado pero importante dominio, el Ritmo de Duraciones pensamos haber realizado un paso apreciable: reconocimiento del necesario balance harmonioso entre Orden y Desorden, una introducción y definición de la Disonancia Rítmica de un ritmo de duraciones, tanto para los golpes individuales como para el ciclo completo; basado en ella, hemos intentado una definición de ‘buen' ritmo; una distinción preliminar entre golpes importantes y de relleno, y un método para estimar ritmos racionales a partir de grabaciones. Estos conceptos han sido aplicados, como decíamos, al estudio de la Txalaparta, que carecía de un marco teórico desde el cual contemplar y entender su toque.
Todos estos conceptos han sido reconectados, a pesar de su incompletitud,
con aquel antiguo y bello paralelo entre Tono y Ritmo, los pilares de la
Música, y enlazan esta teoría con la prestigiosa línea de pensamiento que
considera el Número como la base del Arte, incluso de la Naturaleza.
BIBLIOGRAFÍA
BARKER, A.(ed). Greek musical Writings,II: Harmonic and Acoustic Theory. Univ. Pres. Cambridge,.1989
BACKUS, The Acoustic Foundation of Music. Norton, N.York,1977
BELTRAN, J.M.
(1884) (ed.) Grabación privada ***.
(1988) "Txalaparta@. Cuadernos de Etnología de Navarra, n1 52,. Pamplona, 1988:419-439.
(1991) (ed.) "Euskal Herriko Soinu Tresnak / Instrumentos musicales del País Vasco@. Gobierno Vasco. Grabación en Compact Disk:: L.G.55-1166/91-KD.1991: pista 9.
(1996) Soinutesnak Euskal Herri Musikan/ Los Instrumentos de la Música Popular Vasca. Egin, Donostia***
BENADE, A.H. Fundamentals of musical Acoustics. Oxford, N.York, 1976
FERNÁNDEZ, R., FÚSTER, A., JORDÁ, S., SÁNCHEZ, F.J. S.E.T.S. v.1B. Manual de Referencia. S.E.T.S. v.1B. Manual del Usuario. S.E.T.S. v.1. Listados de tratamiento de palabra. Lab.Tratamiento de Palabra y Música, I.E.C., C.S.I.C., Madrid, 1990.
GEVAERT, F.A. Histoire et Théorie de la Musique de l'Antiquité. G.Olms, Hildes 1965
GUETTAT, M. La Musique Clasíque du Maghreb. Sindbad, Paris, 1980
HAKKI, I,Ö. Türk Mûsikîsi Nazariyati ve Usûlleri. Ötüken Ne, Istanbul,1984
OLSON, H.F. Music, Physics and Engineering. Dover, N.York,1967
RADEMACHER, H. & TOEPLITZ, O. (1970): Números y Figuras. Madrid: Alianza:163
ROEDERER, J.G. Introduction to the Physics and Psychoacoustics of Music. Springer, N.York,1979
SACHS,K. Musicología Comparada. Eudeba, B.Aires,1966
SÄNCHEZ. F.J.:
(1977) "Application of Dissimilarity and Aperiodicity Functions to Pitch Extraction and Voiced‑Unvoiced Decision in Speech" , Madrid,9. ICA Congress.
(1979) Tratamiento Señales Pseudoperiódicas. , Madrid, Ph.D. U.P.M.
(1990). "El motivo: apuntes de la asignatura Acústica III", Doctorado. Cent. Sup. Invest. Prom. Música, U.A.M., Madrid.
(1992a) "Number as Music Builder: Sonance". Symp. Mús.Informática y Psicoac. Delfos (Grecia).
(1992b) ARitmo como Motivo, Sonancia y Complejidad". Apuntes asignatura Musicología Sistemática V, Doctorado. Centro Superior para la Promoción de la Música, U.A.M., Madrid.
(1992c). "Las Músicas Modales Cultas y Populares". Apuntes asignatura Etnomúsicología I, Doctorado. Centro Superior para la Promoción de la Música, U.A.M., Madrid.
(1993a) "Beyond 12‑interval temperament in Arab and related musics'. IV.Symp. Mikrotöne. Esc. Mozarteum' Salzburgo (Austria). 1991. Pub: en Musikedition Nymphenburg 2001, pp. 263‑301.
(1993b) APsicología del Ritmo Turco y Arabe". Symposium Multidisciplinar sobre Ritmo. Cátedra Salinas de Musicología. Universidad de Salamanca. junio.
(1993c) "Música Turca y Arabe: relaciones estructurales con el Flamenco. Apuntes Curso de Ampliación musical, Universidad de Alcalá de Henares. Alcalá‑Madrid, abril 1993.
(1994) "ESCALA, Automatic Measurement of Oriental Scales". Proceedings of ICEMCO,94. A. Ubaydli (ed.), Univ. of Cambridge. London.
(1995a) "Recitación de un poema español". Memoria interna. LTPM, Madrid.
(1995b) "Txalaparta. Breve Estudio Acústico-musical". Txistulari, n1.162. Donostia. Marzo,.
STRANGEWAYS. F. The Music of Hindostan Orie.Rep. Delhi 1975
TOBIAS, J.V. Foundations of Modern Auditory Theory Ac.Pres N.York,1970
WINCKEL, F..
(1960) Vues Nouvelles sur le Monde des Sons. Dunod, Paris.
(1967) Music, Sound and Sensation. Dover, N.York
APÉNDICE. DOS TEORÍAS NUMÉRICAS DE LA CONSONANCIA
A1. Euler.
El gran matemático Euler se interesó (entre muchos otras temas) por el problema de la consonancia musical y elaboró una interesante teoría basada en la descomposición en factores primos de los números que expresan las relaciones de frecuencia de los sonidos entre sí.
Si un número natural A es expresado como producto de primos, Euler define su grado de complejidad C(A), como:
i i A = P pi ai entonces: EC(A) = 1 + S ai@(pi‑1) (1)siendo pi (p sub i) los factores primos de A, ai (a sub i) sus exponentes, y P y Σ los signos de producto y sumatorio. Por ejemplo la complejidad de 8 (2 al cubo)es 1+3.(2‑1)=4 mientras que la de 9 es 1+2(3‑1)=5; es decir 8 es más sencillo que 9'
El grado (de disonancia) de un intervalo reducido a números mínimos es simplemente el grado del producto de numerador y denominador. Así, la quinta 3/2 tiene el grado 4, igual que el de 2x3=6 (1+2+1), la cuarta 4/3 tiene 5 (=1+2+2), etc.
En general la disonancia de un conjunto simultáneo de notas, como un acorde, vendra dado por el grado de complejidad del cociente entre el mínimo común múltiplo y el máximo común divisor de sus frecuencias:
/ m.c.m (a,b,c,.)\ ED (a,b,c,..) = EC ( ─────────) \ m.c.d (a,b,c,.) /Por ejemplo, las frecuencias 220:330:440, la‑mi‑la, tienen una disonancia como acorde igual al grado de disonancia del cociente (3H4H110)/110 = 12, que es 1+2H(2-1)+1H(3-1) = 5; y lo mismo los acordes do‑sol‑do o mi‑si‑mi. El acorde mayor en su forma fundamental, como do‑mi‑sol, reducido a cifras sencillas, tendrá siempre unas frecuencias proporcionales a 4‑5‑6, lo que nos lleva a una disonancia igual a la complejidad de 60, que es 9, mientras que el menor, la‑do‑mi, proporcional a 5/6‑1‑5/4, o sea, 10‑12‑15, tiene un grado como el de 60, otra vez 9.
Otras inversiones de estos acordes pueden variar su disonancia: por ejemplo, el caso sol‑do‑mi, proporcional a 3/4‑1‑5/4, o 3‑4‑5, da 9, como antes (a partir de 60) pero mi‑sol‑do, 5/4‑3/2‑2, o 5‑6‑8, da 10 (el de 120, 1+3+2+4 = 10).
La teoría de Euler parece coincidir bastante bien con el sentimiento común del músico, y por otra parte ofrece una medida de una cualidad aparentemente tan elusiva al número como la consonancia. Es una interesante teoría, y lo es más aún por su sencillez y elegancia (incluso trascendencia, al enlazar con las antiguas teorías pitagóricas).
Es posible encontrar una relación entre esta estimación de esta consonancia aparentemente sólo aritmética, y la percepción basada en la neurofisiología. En efecto, un sonido con tono tiene una frecuencia de repetición de una forma de onda, cuya duración es un período. La audición simultánea de dos sonidos de períodos primos entre si creará una forma de onda cuyo período será el producto de aquellos; es decir habrá un tiempo de concepción simultánea, el período de la onda, tanto mayor cuanto más complicada es la relación entre esos primos. Y la complicación --disonancia-- será tanto mayor cuantos más sonidos primos añadamos. Las figuras 4 y 5, comentadas como ritmos, son igualmente válidas para ilustrar estas relaciones tonales: el caso tonal es idéntico, pero en escala temporal mucho menor, al de un ritmo, tanto más difícil de comprender y concebir, cuantos más golpes (irreductibles) contenga.
| intervalo razón cents ED DE1 DE\/2 DE2 DE2n | |
Fig.22. Valores de Disonacias Euler y Esencial para
los intervalos más usuales. |
Helmholtz extendió estas relaciónes de sonancia, basadas en las frecuencias fundamentales de los tonos de varios sonidos, a sus armónicos. Ahora la complejidad se da entre los componentes de las familias de armónicos de cada sonido, complicándose la cosa; no obstante, él trata el tema en el dominio de las frecuencias, considerando los batidos o chirridos que armónicos de frecuencia vecina producen en el oído, centrándose en el aspecto fisio-neurológico, y alejándose ya de la visión numerista de Euler.
En el cuadro de la fig.22 pueden verse las disonancias ED (según Euler) de los principales intervalos supernumerarios --es decir, del tipo (n+1)/n-- que forman la base perceptiva de nuestras escalas. Se incluyen otros datos a los que volveremos más tarde (todos ellos calculados mediante nuestro program Euler16), El lector juzgará si estos números corresponden a su estimación, recordando, eso sí, que su práctica musical ha influído en su valoración natural o primitiva [Sánchez, 93,94,95].
A2. Esencial
Debido a la necesidad de conseguir determinadas propiedades matemáticas (intervalos como vectores en un espacio vectorial y disonancia como distancia en ese espacio, definiendo así un espacio métrico) introdujimos (Sánchez, 92,93) una variación de la medida de la disonancia por Euler: suprimimos el sumando
>1', lo que no afecta a la jerarquía relativa de los intervalos en cuanto a su disonancia; por otra parte, generalizamos la noción para diversos exponentes de los factores primos involucrados. Definimos, pues la Disonancia Esencial de un entero positivo A como: i i A = P pi ai entonces: CEr(A) = ( S ai@ (pi‑1) r ) 1 / r 1<=r<infinito (3)siendo r un exponente real que pondera los primos diferentemente según su tamaño; pi (p sub i) los factores primos de A, ai (a sub i) sus exponentes, y
P y Σ los signos de producto y sumatorio. Además, similarmente:El grado de r-Disonancia Esencial de un conjunto de notas, como un acorde, vendrá dado por la r-Complejidad Esencial del cociente entre el mínimo común múltiplo y el máximo común divisor de sus frecuencia
/ m.c.m (A,B,C,..)\ DEr (A,B,C,..) = CEr (N) = (─── ─── ────) \ m.c.d (A,B,C,..)/Por ejemplo, las frecuencias 220:330:440, la‑mi‑la, tienen una disonancia como acorde igual al grado de disonancia del cociente (3
H4H110)/110 = 12, que es 2H(2-1)+1H(3-1) = 4 (era 5 para Euler); y lo mismo los acordes do‑sol‑do o mi‑si‑mi. El acorde mayor en su forma fundamental, como do‑mi‑sol, reducido a cifras sencillas, tendrá siempre unas frecuencias proporcionales a 4‑5‑6, lo que nos lleva a una disonancia igual a la complejidad de 60, que es 8 [(2H(2-1)+1H(3-1)+1H(5-1)], mientras que el menor, la‑do‑mi, proporcional a 5/6‑1‑5/4, o sea, 10‑12‑15, tiene un grado como el de 60, otra vez 8: se observa que ambos acordes resultan igualmente consonantes o disonantes, lo que coincide con la apreciación general.Otras inversiones de un acorde pueden variar la disonancia: por ejemplo, el caso sol‑do‑mi, proporcional a 3/4‑1‑5/4, o 3‑4‑5, da 8, como antes (a partir de 60) pero mi‑sol‑do, 5/4‑3/2‑2, o 5‑6‑8, da 9 (el de 120, 3+2+4 = 9): es una inversión ligeramente más disonante que la forma fundamental.
En el cuadro de la figura 22 aparecen las DEr para r =1 y 2, así como la mitad de DE1 y DE2 normalizada para igualar su disonancia con DE1 para la quinta (3:2).
A3. Interpretación musical del número N
El número N, definido en el párrafo anterior como el cociente entre máximo común múltiplo y mínimo común divisor de las frecuencias de las notas oídas simultáneamente, tiene una interesante interpretación sonora y musical. Primeramente, se comprende que dividir por el m.c.d de las frecuencias, elimina la tesitura del acorde, reduciendola a una escala común: de esta manera se igualan acordes en octavas diferentes. por ejemplo: N sería igual para los acordes do3-mi-3-sol3, de frecuencias: 262:262
H5/4:262H3/2, que do5-mi-5-sol5, (1047:1047H5/4:1047H3/2): en efecto, para ambos, N1 = (262H4H3H5) / (262) = 3H4H5; y N2 = (1047H4H3H5 ) / (1047) = 3H4H5, son iguales, la tesitura no influye en la disonancia esencial; así, toda tríada proporcional a 4-5-6 tiene igual N y por tanto igual DEr.A.4 Sonancia de un ritmo
| situ 1 n tp ┴─┴─┴@┴─┴─┴─┴@─┴─┴@┴─┴─┴ orden n-1 o1 o2 o3 2n-1 |
| Fig.23. Notaciones en un ritmo inserto en un compas de n tiempos primos.. |
Consideremos pues un ritmo como un conjunto de golpes insertos en un compás (fig.23) de al menos 3 CP o tiempos primos (2 no permitiría la percepción del patrón formado por los golpes, tanto si eran 2 como si era 1). Tendremos pues desde 1 a n-1 golpes (n golpes en el compás de n vuelve a resultar un tempo sin compás). Este conjunto de golpes que componen un ritmo, forman lo que podemos llamar un acorde rítmico, un conjunto de sucesos con una sonancia colectiva que depende de las de todos ellos, al igual que ocurre en un acorde de tonos o notas. Por lo tanto, adaptando la fórmula (4) al dominio temporal rítmico encontramos:
Sea un ritmo R definido como la presencia (golpe) o ausencia (no golpe o silencio) en cada uno de los n tiempos primos comprendidos en un compás; si tenemos m golpes con órdenes sucesivos o1, o2,..., om, para un ritmo R definido mediante:
R = ( n, (o1,o2,..., om) ) 2<n 0 < m <=n 0<= oi < n (5)
entonces definimos su disonancia esencial rítmica como la r-Disonancia Esencial de las frecuencia rítmicas de esos golpes, definidas como el cociente de su orden dividido por n, número de tiempos primos en el compás, o sea:
| / m.c.m (o1/n, o2/n, ..., om/n) \ DERr (R) = CEr (──────────────────── = (6 \ m.c.d (o1/n, o2/n, ..., om/n) / |
El orden de un golpe en situación i en un compás de n CP
=s se define como su situación respecto al principio del compás anterior, comenzando a contar en 0, o sea, vale n+i-1. Véanse las figuras 23 y 7, y el párrafo 1.5, para ilustrar estos puntos y aplicar estas definiciones.A5. Sonancia aproximada
Todos los conceptos anteriores, basados en el número entero y sus relaciones, número racional, pueden ser aplicados asimismo a los números de la llamada realidad si aproximamos los números que en ella aparecen, los números reales, mediante racionales cercanos, según se indicaba en la sección homóloga (y homónima) 1.6. En los párrafos siguientes buscaremos métodos para lograr una buena aproximación.
Pero en el caso que nos ocupa interviene un elemento adicional: no sólo esa calidad de la aproximación cuenta, sino además, los enteros que entran en juego (numerador, denominador) deben ser lo más sencillos posible desde el punto de vista de su complejidad, o sonancia, ya que ésa es la simplicidad desde el punto de vista (de oído) perceptivo. Así que quebrados con números simples deben ser preferidos a otros quizá menores, pero más complejos --ya vimos cómo 7 es más complejo que 8, que 9 y que 10.
Si se trata de varios números, la buena aproximación perceptiva será aquella que produzca números simples.
De modo que intentaremos racionalizar varias cantidades, convertir varios reales en racionales, o lo que es lo mismo, encontrar una unidad o módulo de medida respecto a la cual loos reales son múltiplos. El problema es resoluble exactamente algunas veces: pensemos en w, 2w, 3w...que admite obviamente la unidad real w y proporciona medidas exactas enteras, 1, 2, 3. Pero en general no encontraremos esa sencillez, debido a las razones antes expuestas, por lo que convendrá suavizar las condiciones del problema, que quedará planteado así:
Se desea encontrar un número real del cual varios reales dados son aproximadamente múltiplos.
Ya se comprende que ahora el problema se transfiere al adverbio aproximadamente. En efecto, siempre es posible encontrar un real (de hecho cualquiera) que aproxime poco o mucho eses múltiplos: pero claro, los restos serán cualesquiera. Se tratará entonces de acotar esos restos o errores que separan esos múltiplos aproximados de los exactos. Por ejemplo los números 10.1, 20.1, 29.8 admiten el divisor aproximado 10, con errores de .1 , .1, -.2, respectivamente. Podemos entonces definir una medida colectiva de esos restos, y acotar esa medida de modo que sólo cuando la medida de los restos es menor que la cota, será aceptada esa aproximación. Precisamos pues nuestro problema:
Sean los reales a1,a2,...,an. Buscamos un divisor real común a todos cuya error colectivo de aproximación E, sea pequeño (es decir, menor que una cierta cota, C
Mediremos ese error de aproximación como E = ||ei||r, o sea como la r-norma del vector e de errores parciales ei, siendo a su vez esos errores parciales definidos mediante bi =ci*d + ei (ci son los cocientes enteros de dividir los reales bi entre d, y ei el resto real de esta división). El resto ei es, naturalmente, menor que el divisor d. En general estará comprendido entre 0 y d y, considerado como una variable aleatoria uniforme, su valor medio será proporcional a d, y valdrá d/2.
De modo que para comparar diversos divisores convendrá normalizar esos restos ei dividiéndolos por su correspondiente divisor medio, d/2. asimismo conviene normalizar respecto al número de reales ai, para evitar que crezca el error con ese número. De modo que en lugar de la r-norma E calcularemos la r-media, E, quedando el índice de calidad como:
Qr(e)= Er(e) / (d/2) o sea Qr(e) = 2
( S | ei | r / n ) 1 / r / d 1<=r<infinito (7)donde todos los números que aparecen son reales (sólo serán enteros, positivos, los cocientes). La r-media se calcula sumando todas las potencias r de los valores absolutos de los errores de aproximación, dividiendo la suma por su número, y extrayendo la raíz r. Para r = 1, encontramos la media aritmética habitual de los errores absolutos. Nótese que al dividir por d/2 hemos normalizado esa media, con lo que hemos encontrado la cota C buscada:
Qr(e) < 1 (9)
Definimos ahora el máximo común divisor aproximado, mcda, de esos reales como:
El mcda de varios reales ai es aquel divisor entero d que entre dos límites, presenta menor Qr.
Parece intuitivamente razonable esperar que los divisores enteros del mcda sean también buenos divisores porque a su vez aproximan bien a d. Incluso algún múltiplo de d puede ser también buen candidato. Pero ahora es decisorio el parámetro Q, que compara entre sí esas aproximaciones al colectivo ai.
Ahora bien, )cómo buscar esos buenos valores? )habrán de calcularse esas calidades para todos los posibles divisores?. Ya se ve que eso es imposible, ya que son infinitos, y, tomado sólo algunos igualemnet espaciados, al menos largo. Veamos cómo algunos razonamientos y técnicas sencillas nos permitirán encontrar más rapidamente los racionales buscados para dos valores reales, aproximando su cociente, otro real, mediante un quebrado.
A6.Buenas aproximaciones de un número real mediante fracciones contínuas
Desde el punto de vista aritmético, esta operación de asimilación de un real, cociente de otro dos, a un racional, cociente de enteros, se realiza mediante las sucesivas reducidas de una fracción continua. Como es sabido, estas reducidas aproximan el número real dado mediante números racionales de exactitud y tamaño (valor de numerador y denominador) crecientes; de modo que podemos decir que la mayor exactitud queda compensada o penalizada por el manejo de números mayores. Un compromiso es pues necesario, surgiendo el concepto de calidad de una aproximación. Por ejemplo, dos aproximaciones conocidas de antiguo del número p, 22/7 y 355/113 son consideradas muy buenas, lo que quiere decir que con números bajos logramos gran aproximación: p=3.141592..., 22/7=3.1428..., 355/113=3.141592... ).
num aprox deno error: abso, e (e*deno2) ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑ ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑ p = 3.141592653589793... 355 / 113 2.67E‑07 0.003 22 / 7 1.26E‑03 0.062 3 / 1 1.42E‑01 0.142 1146408 / 364913 1.61E‑12 0.215 Semitono temperado = 1.059463094359295... 1 1 5.95E‑02 0.059 196 185 3.63E‑06 0.124 18904 17843 4.12E‑10 0.131 18 17 6.40E‑04 0.185 Número de oro =(1+raiz2(5))/2=1.618033988749895... 2 1 3.82E‑01 0.382 5 3 4.86E‑02 0.438 13 8 6.97E‑03 0.446 34 21 1.01E‑03 0.447 Raiz cuadrada de 2 = 1.414213562373095... 3 2 8.58E‑02 0.343 17 12 2.45E‑03 0.353 665857 470832 1.59E‑12 0.354 99 70 7.22E‑05 0.354 Fig.24. ‘Buenas' aproximaciones de varios números reales importantes mediante racionales, ordenados según su calidad.. Aplicamos por lo tanto la teoría de las fracciones contínuas y sus reducidas para aproximar reales o racionales grandes mediante racionales pequeños, o sea, con términos (numerador y denominador) pequeños. En la fig.24 aparecen diversas aproximaciones a varios importantes números reales obtenidas mediante nuestro programa Fraco4 (97) y ordenadas de acuerdo con un parámetro de calidad que definimos como el error absoluto multiplicado por el cuadrado del denominador. Este parámetro empíricamente hallado, puede justificarse a partir de cota de aproximación de cualquier real mediante una fracción o quebrado, que afirma que el error de aproximación es, en valor absoluto menor que la inversa del cuadrado del denominador del quebrado aproximante (Rademacher, 70); multiplicando por el denominador de la cota, obtenemos la igualdad:
| real - m/n | . n2 < 1 (10)
Puesto que todos los reales tienen infinitas aproximaciones que cumplen la desigualdad anterior, calcularemos aquellas de ellas cuyos términos no sean muy grandes, las cuales serán considerados buenas aproximaciones, y de ellas, consideraremos como la mejor aquella cuyo primer miembro es más pequeño. Encontramos así un segundo índice de calidad, Qb, cuya expresión, comprendiendo que 1/n es de hecho el intervalo unidad en que se divide el campo numérico, que llamamos antes d, queda:
Qb =| real - m/n | / d2 (11)
Ese proceso se muestra en la fig. 24, donde se ve cómo todos las aproximaciones encontradas cumplen el criterio, pero algunas lo hacen de manera extremadamente buena, como la primera aproximación de ..os númeralg.
A7. Buenas aproximaciones de varios reales.
Si ahora generalizamos para varios números, como hicimos en (7), encontramos la expresión para el índice de calidad de las buenas aproximaciones, mediante las diferentes medias de los Qb de cada número aproximado:
Qbr(e)= Er(e) / d2 o sea Qbr(e) =
( S | ei | r / n ) 1 / r / d2 1<=r<infinito (12))Por qué dos criterios, uno de ellos mucho más estricto?. El motivo reside en que todos los grupos de reales cumplen el criterio (7), para todo divisor, pero sólo algunos grupos de reales cumplen el criterio (12) para algunos divisores, los buenos divisores. Son pues dos cotas, una absoluta, otra para casos privilegiados.
A8. Granularización del espacio. Tiempo y frecuencia.
Un dominio (dos en realidad) donde surge el problema anterior es la música, en sus rasgos y subdominios asociados, tiempo y frecuencia. En el primero, una serie de sucesos perceptuales, como golpes o notas, cuyos instantes de ocurrencia no guardan una regularidad estricta debido a errores de ejecución o de medida, han de ser llevados, interpretados como sucediendo dentro de una discretización o granularización del tiempo, la cual está ligada en música a conceptos tales como tempo, chonos protos, motor, etc. Esta granularización asímila esos instantes de aparición a uno de esos granos o átomos temporales que rayan como un canevas el tiempo. La percepción reduce y simplifica esas cantidades inconmensurable entre sí, a un sistema relativamente sencillo donde todos las duraciones (intervalos entre golpes) son múltiplos de ese grano temporal. La percepción de duraciones se hace simple, pues se pueden contar el número de granos (subdividir) tanto al hacer ritmo como al percibirlo.
En el dominio del tono o frecuencia, la aparición de escalas con intervalos variados hace imposible reducir esos intervalos a un múltiplo de otro menor común para todos. El proceso de reducción de esos varidos intervalos a múltiplos de ese grano tonal es llamado temperamento, siendo el valor del grano variable con el sistema musical: semitono para la música occidental (12 granos por octava), coma Hölder para escalas más naturales (53 gpo), dieciseisavos de tono en Aristoxeno y en algunos microtonalismos modernos, 31 en Huygens, etc.
Vuelta al Principio Última actualización: Thursday, 20 de February de 2014 Visitantes: