Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.

This page is being developed: I am sorry for errors, duplications  and unfinished subjects.

 ADA Algorithm for Pitch Estimation (included in   An_aadf_pitch_estimator  and written with Enrique Tomás)

See a description of the algorithm here.

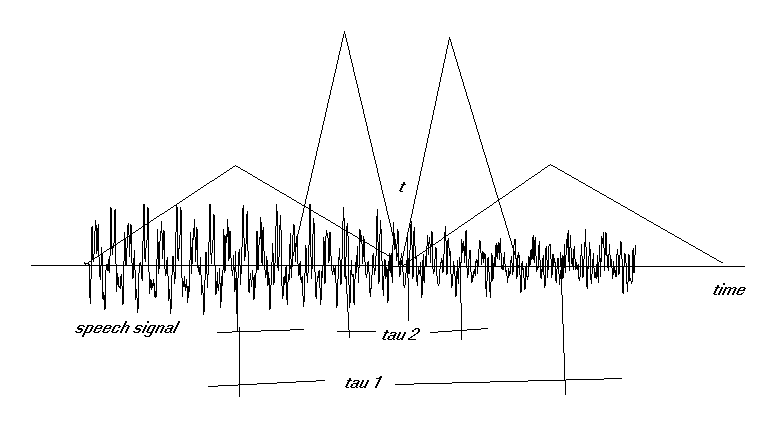An actual placement of windows to calculate the ADF in two points, that is for two values of delay t .

1. We have the signal in a vector, Signal(n).

2. We select an element  t, advanced enough to allow before it a window equal to the maximum period expected (lower pitch).

3. We calculate the Autodissimilarity Function for this moment t

    3.1 We select two new points t1 and t2, at equal temporal distance of t, that is t - t /2 and t + t/2. The time interval between this two points is therefore t
.    3.2 Centered on t1 and t2 we place two equal windows (see possible shapes below) and multiply   each sample inside those windows for the window value in this point. In that way we have selected two signals vectors that we are going now to compare.

    3.3 We calculate the energy (some of the samples or a more sophisticated measurement) of each vector, its norm, and also the norm of the difference of those vectors (We can also find the difference between the vectors before and apply the window to it saving computer time) .

    3.4 With those values, N1,  N2 and D, we calculate the Autodissimilarity between the signal segments centered in t1 and t2, for this particular value of  t
    3.5 We repeat, the steps 3.1 to 3.4 for two new points t1 and t2 now separated a delay  t
 prime, obtaining thus a new value of the dissimilarity t

    3.6 Changing  t we will obtain new values of this dissimilarity, that is the dissimilarity function with the variable  t. Since we obtain all the fragments from the same signal we call it Autodissimilarity function, ADF.

    3.7 The minimum of this ADF will point two the  t  value for which the similarity between the pair of fragments were maximum: this happens for a  t equal to the period in a periodic signal because all the signal periods are equal, mean while the similarities for t different of the periods will be lesser, and ADF will be bigger.

3.8 Therefore the minimum of ADF points to a  t  equal to a period of a periodic signal, or to the pseudo period of an pseudo periodic signal, in a particular moment t.

    4. For another moment t' , we will repeat the steps 2 to 3.8, obtaining in that way the pseudo period of another moment in the same signal.

    5. Repeating this in equal time intervals, we will find the pitch signal corresponding to the original signal.

    6. And that's all for the moment. But there are

Problems and Strategies