A NUMERICAL THEORY OF RHYTHM APPLIED TO ORIENTAL MUSIC ANALYSIS
ABSTRACT. While classical theory of rhythm was developed along with tone, in modern times, especially in the West, rhythm has become simpler, at least compared to non Western music. Theory and practice in this field are thus lacking in development and understanding. This paper seeks to fill this gap, establishing a bridge between perception, number and rhythm, as we have already done for tone and melody [Sánchez, 93a]. Following these former tonal steps, a new numerical theory of rhythm is now introduced, and its model applied to the analysis of classical Oriental rhythms and metres. A method to estimate rhythms from the audio recorded signal is also presented and computer-implemented, constituting a tool for automatic rhythmic analysis, as is shown with some examples from Folklore. An appendix is reserved for the simple mathematical background needed for these theories. We hope this paper will lead to a better understanding of our rhythmical perception, aesthetic impression and pleasure.
Back to Main Page
INDEX Abstract INTRODUCTION 1. RHYTHMIC THEORY 1.1. Order and disorder 1.2 Rhythm 1.3. Introduction to a rhythmic theory 1.4 Rhythmic Sonance 1.5 Sonance of a rhythm 1.6 Notation and empirical rules of application 1.7 Tentative approach to define a 'good' rhythm 1.8 Approximate Rhythmic Sonance 2. APPLICATION TO ORIENTAL RHYTHMIC AND METRICS 2.1. Oriental rhythms and their rhythmic dissonance 2.1.1. Arabic Rhythms 2.2. Oriental meters and their rhythmic dissonance 2.2.1. Arabic metres 2.2.2. Persian metres 2.2.3. Classical Western metres 2.3. Folkloric rhythms: automatic transcription and rhythmic dissonance 2.3.1 Percussion of Gnâua. 2.3.2. Percussion of Basque Txalaparta. 3. CONCLUSIONS REFERENCES APPENDIX. TWO NUMERICAL THEORIES OF SONANCE A.1 Euler Sonance A.2 Essential Sonance A.3 musical interpretation of the number N A.4 Sonance of a duration rhythm A.5 Approximate Sonance
Numerous tonal theories have been proposed from classical Greek times until the present, but the rhythmic theories, which were developed along parallel lines at the time, have since been much less frequent, having almost disappeared in our Western modern environment. Does that gap coincide with a gradual rhythmic simplification (impoverishment?), perhaps convenient for the enormous development of the tonal complexity (modality, harmony, timbrics), the orchestra's size and that of the hall that houses it? In any case, an intricate and quick rhythm, simultaneously executed by a hundred interpreters, would not be easily well interpreted and perceived. Be that as it may, modern Western music has derived toward symphonies and concerts that primarily use the simplest measures, whatever its tonal complexity.
If we return to the Oriental world, we find smaller ensembles
and soloists
the great Arabic orchestra is perhaps not its best
representative, in spite of its popularity that introduce larger rhythmic (and
tonal!) subtleties, either in the numerous rhythms coded in their musical
systems, or in their solos taqsim, layali, that are endowed
with a great finesse, less repetitive than the coded.
On the other hand, folkloric music presents even more complex rhythmics, often the more primitive the culture from which it emanates is deemed to be, the more this is the case. Indeed, African rhythms and their descendants, such as those found in Cuban or Brazilian Black music, are so difficult sometimes for the Western ear, that it simply does not perceive them, and supposes that there is either no rhythm in this music or that there is one which cannot be grasped; while interpreters and listeners from that particular culture, have no difficulty in following it, dancing it with ease and pleasure.
But frequently there is neither a theory nor a notation for folklore, and to understand what happens, rhythmically and musically, we need to introduce basic concepts of musical execution and perception that will serve us as a reference framework or context, in order to find how these rhythms are inserted in this more general system.
As our musical paradigm lacks flexible rhythmic concepts which form the aforementioned framework, we shall therefore introduce a rhythmic theory which allows us to understand this and other temporal manifestations, such as the rhythms in other musical systems and the metres in classical poetry.
That is to say, we lack theories, we lack perceptive subtlety of Rhythm, and we also lack technological tools that analyze musical samples to estimate, to automatically calculate the corresponding abstract rhythm. This article will endeavor to partly remedy this shortcoming with respect to the first and final gap, in the hope that the second one will be filled as the listener, musician and Western musicologist understand that our music is only one, and in some respects not the best, among dozens of others: only this grandiose group can properly be described as Music, with a capital letter.
In the following pages we will begin polarizing music between order and disorder, and their representatives, number and expression. Next we define the concept of rhythm and introduce a psychological justification for the application of number to the rhythm and its parts, integrating them. We then propose a new approach to measuring dissonance or rhythmic complexity; we apply it to some oriental and non-oriental rhythms, showing the relationship between those measurements and their musical qualities. We also contemplate from this perspective some classical metres. The model is then applied to the automatic estimation of some recorded rhythms, showing its utility in discerning their underlying patterns, even when our hearing is not capable (outside its context, clearly) of perceiving it; this method has been used to discern the rhythmics of Basque txalaparta in a recent paper [Sánchez and Beltran, 1998]. We reserve for the appendix the whole mathematical apparatus which, although simple, might not interest the non specialized reader.
Intending to study music, or, rather, those aspects of it able to be conceptualized, let us reflect on what Music is and on how it differs from other performance arts. Music is sound, unlike the visual arts, which fall beyond the scope of this topic although concomitant sensations, such as repetition, ratios, motives, etc, establish bridges between the former and the latter; but this is a more general matter covered by synesthesia. Limiting ourselves to the world of sound, we find a wide group formed by speech and music, and inside the first, but close to the second, poetry. But we find at once a radical difference between these two branches with regard to their production: while in speech one mentions concepts or ideas of the external world (which constitutes language), in music one mentions or better, invokesnon conceptual notions. We can say that, in speech, we say things about the world outside, while in music what is said comes from the inside. What then defines music and differentiates it from its partners, speech and poetry, to which it perhaps gave birth, or from which perhaps derives?
If we consider the characteristics or sound features that intervene in speech and music, we observe that both use these independent separately variable elements: pitch, or height of the sound, intensity, or its strength, quantity, or the fragmentation of time in units of different durations, and timbre, or color of these segments; all form a chain or series of changing segments, to convey what is to be expressed.
As the sound features that characterize speech and music are alike, they must be distinguished by their use: indeed, what separates music from similar arts is particularly the introduction of (integer) numbers: it is Number, the measurement of those features, that makes music Music, introducing integer relations, ratios among those measurements, creating Harmony in a general sense and also in the specifically musical one; we will see how in the appendix. But it is already comprehensible, in an immediate way, that simple ratios among durations of the temporal segments or units that we call notes or strokes, provide a regularity on which the feelings and the notions of tempo, measure and rhythm depend, these concepts being absent in natural speech, at least with that degree of accuracy. And, from the point of view of tone, contrary to the continuous variation of all the frequencies along their tonal scope tessitura that the prosodic curve describes in natural speech, in music and song, pitch remains steady for a while, and this only in a small number of tones and frequencies (the notes of the scale): and these simple ratios between these frequencies or tones equally produce specific and preferred intervals (octave, 2:1; fifth, 3:2; fourth, 4:3...) to build scales and chords. These regularities are what resonate inside us, what 'tell' us things.
Therefore music, to become Music, gives up the infinite and continuous variety of durations and tones, and limits itself voluntarily, to build, in this limited universe, more and more complex forms. And this is not denied by the evolution in ways and styles: they change, it is true, but only to be substituted by newer ones.
Why this self-limitation? Our answer can be found in the perception each sensory device through which we perceive. It is an evident fact that we attribute subjective measurements of the aforementioned features in the sound event (that is why we deliberately use them) and it seems a proven fact that we are only able to perceive simple relationships directly, that is to say of 1 to 2, of 2 to 3, perhaps of 5 to 4 (let us remember the usual musical measures). So in music we use relationships that we can perceive, and in the perception of such relationships, somehow we all (or almost all) feel what we can not explain (the ineffable), the joy of Music.
But when we speak of numbers in the human perception, we should keep in mind those mechanisms that describe how the ear-mind perceives those numbers. For example we know that octaves are a little bigger than the interval of frequencies represented by the ratio 2 to 1 (1200 cents), mainly in the extreme ranges (extensive tuning of the extreme octaves in the piano, Mel scale). Therefore an octave of ratio 2.01 can be appreciated as well 'tuned' by the musical ear, in those ranges; and all analyses of intervals should take the distortion that the perception imposes on the arithmetic number into account.
So perception influences those measurements, and therefore the numbers themselves. It is the numbers '2' and '3' that are performed and heard, but the perceived '2' and '3', whose values do not coincide, in general, with the physical measurement. Number, vibration and sound are then inextricably united in music, or better still, they make it. We believe that a scientific approach to music should use objective methods of measurement: but these methods should include the transfer function (or filter modifier) of human perception.
However, having established that necessary numerical universe, imposing an order that sustains the musical building, Music, to become an art needs a certain freedom, that allows the composer's, and interpreter's expressiveness, and surprises, interests and arouses the listener. This is done through small variations or shades which, however, do not undermine the stability of the building its numerical structure, such effects as vibrato, tremolo, portamento, accelerando...
Then we can conclude that in Music (and we believe that also in all the other arts) these two concepts, Order and Freedom (or freedom and order, according to the ideology of the moment) necessarily coexist, in permanent conflict: order makes it comprehensible, and freedom, pleasant and interesting. But order alone is boring, and freedom alone does not express anything, and is equally boring; thus, Music can be defined as Prosody (expressive freedom) in Universals (number and order).
The practical musician, the interpreter, aware of the extraordinary complexity of the musical universe, usually distrusts number and other simple notions, considering them simplistic and, in any event, as a limitation to his/her creative freedom, conquered by the Western world to which he/she belongs. Without mentioning the Oriental world, more traditional on the whole and so more faithful to some principles (order), it is necessary to say that the Western musician makes continuous use, without sometimes knowing it, of that numeric simplicity that he might scorn. When sounding a just fifth, or when composing, playing or perceiving a measure of 3 by 4 she/he is making numbers without knowing it Leibnitz defines the Music like a "occult arithmetic exercise of the soul, unconscious of its counting". The practical musician knows, but he does not know that he knows, as the dragonfly is unaware of its flying, but it flies. The object of the theory is in fact to present this empirical knowledge in the form of concepts.
An example of necessary order in the most spontaneous and 'innocent' activity: when children play, they always play at 'something'; and that ' something, is in effect the group of rules of the game, to which the players submit voluntarily for 'enjoyment's sake', since a game without rules would bore them at once. When in the game it is said that ' that is not fair', does that not mean that the rules of the collective game have been violated? Thus, even those in favor of a playful conception of music, should, taking example from children in this case their teachers, admit certain degree of regulation and order.
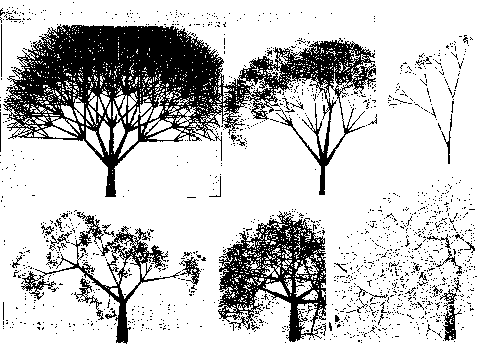 |
| Fig.1. Order and disorder reflected in these trees. |
Another instance may be seen in Fig.1: extreme examples of order and number captured in form, as in music, are observed; one with a high degree of order, whose rigor drowns the aesthetic impression, another with high disorder, which confuses and drowns again the aesthetic impression. Between those poles there are several trees, among which the choice is not easy, since it is affected by the individual idiosyncrasy and by the social and historical environment; but the common choice falls within the intermediate group, where order and disorder, number and their violation, coexist in a balanced and harmonious fashion: let the reader observe the figure and choose for him or herself.
We conceive Rhythm as an almost identical repeated pattern, at almost identical time intervals. In sound, this pattern is a group of events (or strokes). The term 'almost' is important: as long as there is likeness, perceptive likeness between the pattern's repeated executions, there is repetition, perceptive 'return', which maintains the sound continuity; so that there are isolated, discrete events in a whole (the rhythm) that remain. As a Muslim mystic wrote "Rhythm is quietness inside movement".
All rhythm is based on the coexistence of two frequencies or repetition rates: that of the pattern, which frequently corresponds to the western measure, and that of a lattice or canvas made of intervals of minimum duration temporal points. This duration was known by the Ancients as chronos protos (CP) or tempus primus, which in modern times corresponds to the duration of the smallest independent beat that appears in a piece of music (we say independent because even smaller durations can really appear as decorations, mordents, trills, etc, without their duration being considered; that is to say, they only appear as appendices of another note from which they take their duration, from which they are 'nourished', we might say).
But the inner pulse of the music, the counting of the interpreter, also uses the Part, an internal organization of the CPs of the measure in small groups of 2 or 3 CPs. The tempo corresponds here to the frequency of repetition of those parts, so creating an intermediate category between the previous (measure and pulse rates); so that in a 9/8 carried out in three equal parts, at 60 dotted quarter notes per minute, the measure repeats itself every 3 seconds, the part every 1, and the subpart (the quaver) or CP, each third of a second; this whenever they are no shorter figures than the quaver, in which case the subdivision would be greater than 9 per measure. Equally a 9/8 considered as 4+5, often the case in Middle Eastern music, requires a pulse or tempo of 9 CP per measure. Hereafter, we will consider only undivided parts, where part and CP will coincide.
We refer to these well-known concepts here because we are trying to find out if the habitual notation, or any other that include these two basic elements, measure and CP, can be applied or not to folkloric rhythms. which, on principle can be neither be affirmed nor refuted. We will later see that s both answers are correct, and both wrong: folkloric music falls between Order and Disorder (remember the 'intermediate' trees).
1.3. Introduction to a rhythmic theory
In the area of the Aegean, in classical Greece first, and with Persian-Arabic theoreticians later, a rhythmic theory emerged together with the theory of melody: both followed similar steps, with homologous concepts as melodic and rhythmic Genera. The parallel between Rhythm and Melody was then well-known; this connection was lost later on in the West, as the tonal construction got extraordinarily complicated on account of Harmony, while becoming oversimplified (impoverished?) regarding Rhythm, until it hardly no longer needed a specific theory (for almost everything was written in simple measures as 4/ 4 or 3 for 4).
One of the major currents of that classical thought was the Pythagorean, that centered in the importance of Number for the understanding of the Universe order (Logos) in general, and of the sound universe in particular.
The musical intervals perceived accurately and with pleasure (consonances) were and are intervals with simple proportions between their vibration frequencies or pitches, or, equivalently, between lengths of the strings or pipes that emit the tones that compose the interval. Thus, there is a narrow relationship between the auditory simplicity of the octave and the numeric simplicity of the rate of frequencies, 2 to 1. With gradually decreasing consonance, it also exists with the fifth (ratio 3:2), the fourth (4:3), the major third (5:4), minor third (6:5), and so on.
Similarly, it is clear that the simplest measures are those represented by small numbers: almost everybody will admit that the 2/4 measure is the easiest to perform and perceive; closely following, in not such a clear order, we find either 3/4 or 4/4; but 6/8 is simpler than 5/8, even than 8/8 and perhaps than 9/8, and so on. In this way we see how some numbers are simpler than others greater than them. Understandably, the divisibility relationships play an important role here: indeed, 4/4 is 'simple' because 4 is conceived as 2 times 2, that is to say, as 2 by 2; equally 6 is conceived as 3 times 2 (3/4 measure) or 2 times 3 (6/8). So that:
A measure is the more complex the greater its number of parts, and the lesser its divisibility, that is to say, when it admits few and large dividers.
This for the length (in CP) of the measure. But what happens inside the measure? It is evident that some of its strokes act orderly and soothing, while others create tension and disorder. The first part after the bar division is naturally the most relaxing, the one that musically resolves; let us finally say it: the most Consonant, rhythmically speaking. musical pieces generally finish with this part, such as the Tonic does in the tonal domain.
|
C(4/4)
Part or CP:
1
2
3
4 |
|
Fig.2.
Empirical estimation of a value for the Rhythmical Consonance and
Dissonances of each stroke
in a 4/4 measure. |
If we consider a C measure, 4/4, it will be admitted again that the most relaxing part, after the first one, is the third, which corresponds to the middle of the measure. Of the two remaining parts, the second is more consonant than the fourth, which is the most unstable, because this latter prefaces, announces irresistibly the first part of the following measure. It is the anacrusis, of maximum tension and dissonance. Hence almost every musician and listener will admit an ordering of the parts in the 4/4 measure with regard to their consonance as we see in Fig.2, being the numbers, rather that measurements, indicative of a hierarchy. The dissonance will vary inversely (let us make constant the sum of consonance and dissonance: 5, for example). Similarly we would find other hierarchies for other measures, as those we find in Fig.3 where we make consonance and dissonance add up to 3 and 9, respectively. For lack of more information we assign similar consonance and dissonance to parts 2, 4 and 6 in measure 8/4, although is to be expected that they are not exactly so in perceptive practice.
|
3
/ 4
Part and CP 1
2
3 |
|
Fig.3.
Empirical estimation of a value for the Rhythmical Consonance of each
stroke in 3/8 and 8/4 measures. |
We see thus how numbers capture, reflect the common musical experience. Let us try now to find a measurement, at least approximate, of those consonance and dissonance (or 'Sonance' as they will be called from now on, since they point to the same quality, positively or negatively considered),
As with tone, rhythm implies repetition: and in this repetition what counts is the duration of the cycle or repeated period, which is perceived as height pitch in the tonal domain, or as tempo pace, in the rhythmic domain. But what matters is the relative duration of two or more simultaneous periods: it is their relationship or ratio what counts. The more simple is that rapport, as we already know, the simpler their combined perception, the better their rhythmical concord. All this concerns counterpoint, (simultaneous opposition of points or notes of different duration).
|
|
|
Fig.
4. Beating of two tempi in simple frequency ratio. Stroke
coincidences
at the
minimum
common multiple: two simultaneous periods of 2 y 3 seconds compound
another of 6. |
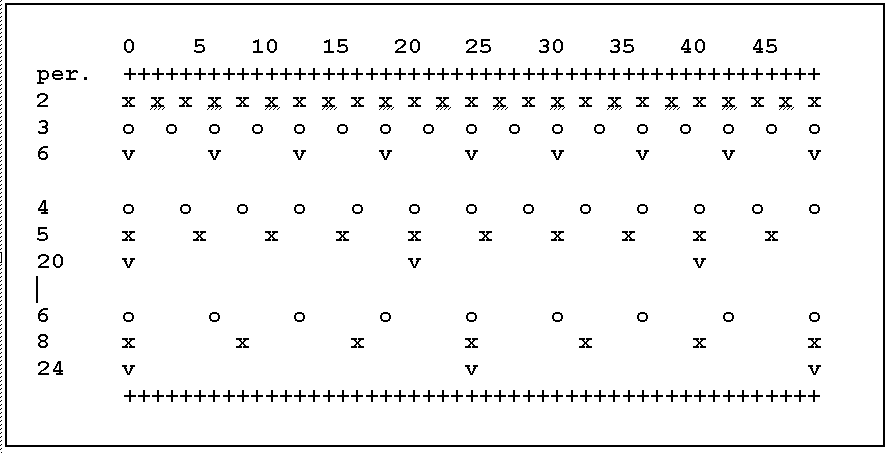
If two tempi of different frequencies are beaten, beginning with a common stroke, two other strokes will coincide again after a time interval equal to the minimum common multiple (m.c.m.) of their periods: for example, when a pair of tempi with periods in the ratio of 2 to 3 are beaten, two blows will coincide once more every three periods of the first tempo, or every two of the second, that is to say, with a period corresponding to 6 units as used in both, as the samples in Fig.4. If the periods are mutual primes, as 4 and 5, we obtain a period of 20, which becomes difficult to follow. On the other hand, if the periods are not mutual primes, 8 and 6 for example, the compound period is surely 24; but these three values, 6, 8, 24 are proportional to 3,4,12; and, if we want no ignore the influence of the time scale in our consideration, the value of the 'essential compound period' is smaller than what could be expected (not the product, 48, nor the m.c.m., which is 24); in fact is 12 which corresponds to the quotient between the m.c.m. (24) and the maximum common divider, m.c.d. (2). This m.c.d acts as a module, an unit of measure.
We will generalize these numerical considerations in the appendix, where an introduction to Euler's estimation of tonal dissonance for simultaneous notes is presented, together with our own modification, called Essential Dissonance (ED). Since tone and tempo are two identical processes repetitions with different periods in more or less simple proportion, nothing prevents us from applying this theory and those tonal measures to our case, rhythm, so defining the Rhythmic Essential Dissonance (RED). Whenever the proportion is simple, which means 'rational', quotient of integers and comprehensible to reason notice the simultaneous numeric-cognitive bisemy of the concept, we will be able to measure the mutual rhythmic dissonance of those two tempi; this we do in the following paragraphs.
Two tempi in proportion 1:1 have an essential dissonance (RED) of 0; in the proportion 3:2, RED= (2-1)+(3-2) =3, etc. that is to say, the same values as those for ED1 in Fig.21, first table of the appendix. We deal then with essentially identical rhythmic intervals to the tonal ones, except for the one mentioned change of time scale. We can speak of rhythmic octaves, fifths, thirds, in the beautiful parallelism known already by the Ancients, when they spoke of melodic and rhythmic genera, as we saw.
|
4
o...o...o...o...o...o...o...o...o...o...o...o...o |
| Fig. 5. A measure of 20/8, obtained with two simultaneous tempi with frequencies in the ratio 5 to 4. |
In this case of simple relationships, we can fill the spaces between the strokes of each of the two tempi with faster beats, as many as their respective periods: in this way, the mentioned pair of tempi become measures, the original beats being the principal ones in the measure, and the newly introduced ones, blows the secondary or 'filling' strokes, as is shown in Fig.5: Each principal stroke and the secondary following it constitute the main parts of the measure; and those parts mark, reflect its rationality, its divisibility. Therefore, in Fig.5, we can say that we have a measure of 20/8, containing quavers either in 4 groups of 5, or in five groups of 4 (five halves).
Let us choose now a measure of four parts, 4/4. Once its reiteration is established in our mind (we will be waiting for the first main beat every four), the appearance of a stroke different from the expected first, will suggests a new repetition that coexists and contrasts with the original rate (which was 4). For instance, if the third part is emphasízed, a new period of repetition of 6 parts emerges, against the 4 of the measure. We have therefore two periods in the ratio 6 to 4, that is to say of 3 to 2: it is a 'rhythmic fifth' whose RED1 we saw to be 3. In turn the remaining parts would bear the following dissonances: first part of the measure, RED1(4:4) = 0, rhythmic unison; second part, RED1(5:4) = 6, rhythmic major third; third part, RED1(6:4) = 3, rhythmic just fifth; fourth part, RED1(7:4) = 8, rhythmic natural seventh. The corresponding Euler dissonances are obtained by adding an unit to the RED1 (see the appendix).
|
4
/ 4
Part and CP:
1
2
3
4 |
|
Fig.6.
Comparison between intuitive y calculated sonances. |
The sequence of opposing dissonances is then: 0, 6, 3, 8. But comparing that list with the values deduced directly from the intuitive estimate of our own rhythmic perception (Fig.6), we find that the ordering, the hierarchy of those values (not the actual values) is identical: first the less dissonant part, then the third, the second and the fourth, with maximum dissonance. Our reasoning has provide us with a measurement of our dissonance perception, whose accuracy would be difficult to check, but that undoubtedly, relates, agrees, and very much, with our inner device of musical measurement.
Once established the dissonance of every part of a measure, it is easy to evaluate their combined effect on a rhythm: those made up mainly of dissonant strokes will be more dissonant rhythms on the whole than those that use more consonants strokes. Both have appeared in all the cultures and times. The first ones are tense and exciting, the other calm and peaceful (usually in combination with slower tempi). Let us compare the two rhythms of 8 parts in Fig.7 (in which xxxx means stroke in that part o CP): it is easily understood, even visually, that the first one is much more simple (and boring?) that the second (clearly, each rhythm has its application according the circumstances of its use, we are not establishing preferences).
Consulting the paragraph A4, in the appendix, we calculate the dissonance (of index r = 1) for both rhythms, finding for the first one (see stroke orders in Fig.7) a value for RED1 of EC1(8/8:12/8:14/8) = EC1(8,3,7) = 3+2+6 = 11; and for the second: EC1(8/8:9/8:11/8:15/8) = EC1(8,9,5,11) = 21, much greater, as was already expected.
It seems clear that, despite taking these measurements only as indicative or orientative (while we delve in their relationship with the human psyche), we already find them useful to predict the effects of complexity and dissonance of each measure in particular, of each beat within that measure, and of the rhythms realized by filling with strokes some of the CP in that measure.
|
||||||||||||||||||||||||
| Fig.7. Two rhythms R1 and R2 with 8 parts and very different dissonance. Each stroke is numbered (third row) with it situation in the measure and with its Rhythmic Order, defined as its order when counting, beginning with 0, from the previous bar. |
1.6 Notation and empirical rules of application
The musical notation of a rhythm is somewhat ambiguous, so some criteria are needed to apply meaningfully the former calculus.
The first and main influence lies in the choice of the stroke that is going to be considered as the first one in the rhythmic cycle, and written down after the bar division. This choice correlates, of course, with a clearly defined psychological choice, well established in the musical practice of the performer. But the listener is often confused about this first part, since anacrusis, felt as 'preceding notes', blurs the otherwise sharp and clear measure beginning. Therefore
The choice of the stroke to be the first in the bar, greatly determines the rhythm dissonance.
This will be illustrated in the examples shown in section 2.
The same happens with the length of the bar: shorter measures give smaller numbers and smaller fractions, so smaller dissonance values. Of course, the shorter possible measure length must be preferred, as perception does, always in search of simplicity to ease its task. But this is possible only when the rhythmic patterns inside the bars, the rhythmic motives, are equal in successive measures; only then the repetition is accomplished. This happens, for example, in the Persian metre of paragraph 2.2.2, where the verse line, 24 parts, can be divided in two equal parts of 12, 8 strokes with identical pattern. Then
The shortest (repeated) measure should be chosen to contain the rhythm.
Another difficulty lays in the different ways used to represent strokes: either a short figure followed by a rest completing a certain duration, or a long figure filling this duration. Therefore, in a measure composed of CP cells, the empty ones will be added to the first preceding non-empty one to calculate its duration. Our method avoids however this problem since:
Only the onset, the beginning of the stroke is considered.
Related to this problem we have another, more subtle: a certain duration can be realized by a single stroke or by a series of them, in what is called a roll; these rolls can be performed very quickly, which is felt as a sustained note, or slower, in which case there a legitimate doubt in considering this group of strokes as a whole or as individual blows. How to solve this problem? We must look at the perceptive reaction, as always. The perception only notes changes (let us think in the regular tick-tack of the clock or in the regular thumping of the train's wheels: after a while we do not perceive them at all, unless we consciously intend to do so; only a change, usually their sudden disappearance, draws our attention back to these noises). Therefore only changing strokes will be noted, only blows different from the previous will be perceived as strokes having individual Sonance attributes. Thus
Only the first of a series of equal strokes will be considered for Sonance calculation and perception.
Any change of the stroke qualities will break the roll: intensity, timbre, any variation large enough to be felt inaugurates another section and gains individuality and Sonance properties. musical notation (primitive, classical or contemporary) helps to assess the presence of these perceptive changes: any written feature implies its conscious consideration, as its coding (sign) confirms, and thus suggests a change from the preceding situation.
It must be noted that two blows are equal only if they are surrounded by identical circumstances, which only happens to the inner beats of a group. Therefore, two strokes are always different, and only in groups of 3 or more equal notes can we apply our roll effect.
1.7 Tentative approach to define a good rhythm
A good rhythm must include in its cycle its measure or bar, peaceful, consonant parts, contrasting with tense, dissonant ones. The cycle must include order and disorder in alternative dominance. The tension must rise and fall (/\) providing jumps big enough to be perceived and felt; the psychological tension must accompany this process in the same way as does tonal Sonance, in chord resolution.
With this criterion we find a trochaic bar as
\-e-q\ to be 'worse' than a iambic one, \-q-e\ , because the dissonance cycles are (0,4) and (0,6); the second one provides a greater dissonance jump, felt as satisfactory, resolutive at the beginning of the bar, meanwhile the first is somewhat dull and less resolutive, it does not 'finish' easily. In the same way, Arabic Duyek \ E-q--eQ-q-\ will be considered a 'good' rhythm, because its dissonance cycle, (0,7,13,3,8) present two contrasting cells,( /\/\) which also contrast between themselves, since the first jump is bigger than the second.1.8 Approximate Rhythmic Sonance
When measuring phenomena that happen in the so-called 'Reality' we never obtain exact values, either because the quantities themselves do not fit into simple numbers, or because measurement errors are made, or still because the measurement itself is imprecise in its nature (for example, the precise measurement of a note frequency would need an infinite time). So we always have approximate or inexact values, with that their mutual proportions will also be inexact and, in general, not able to be expressed as rational numbers (quotient of integers). However, our perception certifies us that consonance and rhythm exist, because we hear them. Moreover, those perceptions are linked to integer values close to the inexact ones we measured: we comprehend and we interpret rhythms of 4, 5, 11 parts, but not of 8.345... parts, we can not conceive them. Equally one thinks by means of integer fractions, such as 'a third', 'a half', 'two fifths'.
It is clear therefore that the perceptive mechanism carries out an operation of approximation of those values in a complex proportion, to others in simpler integer proportion; our inner device adjusts, orders the frequencies heard so that they form a comprehensible, simple group, that is to say, as consonant as possible. This operation will be carried out inside some limits, since experience shows us that from a certain amount of divergence or error, a musical interval stops to be recognizable, and passes in our awareness from a (detuned) interval to another.
This threshold of divergence has great importance, and is influenced by many causes (habit, culture, musical system, psycho-physical thresholds of hearing, etc.) so that their study would take us now far from our present topic.
In the appendix we show the mathematical treatment used to find those simple numbers that approach the durations as measured on actual rhythms.
In our case, once we have found those simple numbers, we can consider them as durations of the intervals among strokes, measured in CPs. Also the comparison between the diverse durations will provide us with the measure o bar in which those sound events are framed; the actual existence of this bar is a possible, but not necessarily actual case, since there are melodies and rhythms without a measure, as the western cadenza and the oriental taqsim.
When we know the strokes situation inside the measure, we will be also able to estimate their rhythmic dissonance by means of the formulae seen in previous paragraphs. In the sections on folkloric rhythms, we will show those estimated measurements, and in the appendix, section A5, the simple mathematical techniques used to carry out that approach. But it can already be understood that we are trying to find a 'measuring rod', a temporal unit, the CP, with which all the time intervals between beats will admit a simple measurement, will be expressed as small multiples of this temporal unit.
In this way, we have been able to evaluate the dissonances or tensions of any rhythm. As promised, we will apply such notions to unwritten rhythms taken from Folklore.
2. APPLICATION TO ORIENTAL RHYTHMIC AND METRICS
2.1. Oriental rhythms and their rhythmic dissonance
The rhythms of the Arabic East and Westcountries and other Middle East musical cultures such as Turkish and Persian, use two main types of timbre of strokes: Dum, long and low sound, hit near the center of a drum's membrane, and Tak, short and with a higher pitch, obtained by stroking the drum near the border. These two sounds contrast one with another, allowing combinations or patterns clearly discernible and able to be memorized. By assigning a duration to each stroke, we will repeat the pattern at equal almost equal time intervals: now we have an Oriental rhythm. Other casual strokes can be added between the former, providing variety, freedom and aliveness to the fixed abstract pattern; an important part of the actual performance, which was called rhythmopoeia in ancient Greek music.
|
---4-\--Q--q----e--Q---q---\ 8 9 11 12 14 |
| Fig. 8. Duyek. RED-23(C(4,9,7,11) |
The above mentioned musical systems count hundreds of these rhythms, usually ordered from the simplest and shorter to the longer and complex. Let us represent here Dum strokes by notes with stems down, and Tak with stems up (some authors use the opposite criterion). Let us represent durations and measure by the usual symbols (some Eastern authors use also boxes, numbers for durations, and other symbols for strokes, sometimes secret). See references in Erlanger (1949-1964), Guettat, (1980), Hakki (1984), Jargy (1971), Kaszim (1964), Karadeniz (1965), Malm (1985), Mahdi (1972), Al-rajab (1961), Reinhart (1969), Sachs (1966), Sánchez (1985, 1992c, 1993c), Strangeways (1975), Touma (1977) and Yekta Bey (1986).
In the following pages we will only consider musical figures related to time and duration: no timbre, no intensity, no tempi will be taken into account; therefore the calculations will ignore Dum-Tak differences, except to break a possible roll effect, according to what we said in paragraph 1.6. These features would add complexity to the pattern, but their inclusion will be left for a future paper.
| 4 \---Q---Q---Î---q----Q----Î---q----Î---\ 8 9 11 12 14 |
| Fig.9. Masmudi al kabir. RED-23(C(4,9,7,11) |
One of the simplest, Duyek, count five main strokes in a cycle of 8 units (CP) in 4 parts. The number 8 admits several dividers, especially 2, which allows, mathematically and perceptually, to find 2 main parts that mutually oppose themselves: the first is tense, syncopated, disordered; the second is calm, simple, ordered. Both contrast and complete each other in a simple cycle of order and disorder, showing us an excellent example of balanced and good rhythm (see 1.7).
| 10--8- \--E--ä---ä---e---ä---Q---e--ä-.-ä--\ 10 13 15 17 10-4 -\-Q---Î----Î-----q----Î-----Q---Q---q----Î---Î---\ 10 13 15 16 17 |
| Fig. 10 y 11: Jurjûnâ y Samâî Takîl. RED-35(C(2,3,5,13,17) |
Masmûdi-al-Kabir is very similar, but for the duration, considered to be double (half speed) and for the second stroke, which is Dum instead of Tak, a fact ignored in our calculus. Therefore, its RED is the same as for Duyek. Note that the different notation long notes or shorts plus rests does not affect the value either (see 1.6.).
A similar case arises with the following pair, Jurjûnâ and Samâî Takîl. Both admit a 10-parts measure, the second one being slower takil, weighted and dividing the third stroke, a Dum, in two, with a slightly greater dissonance. It is interesting to note that, were the note order in Jurjûnâ rotated, so that the bar would begin in the second stroke, the RED should be much smaller, only 10 (RED = EC(10,12,15,18)=10); it would be a simpler pattern, a fact that agrees with informal tests.
2.2. Oriental meters and their rhythmic dissonance
Classical metres in poetry, either Greek, Old Latin, Arabic or Persian, show a rich rhythmic content: generally speaking, they have syllables of two length values: short and long. Shorts are composed by a consonant and a short vowel: [cv], while longs are composed either of a consonant and a long vowel: [cv:], or of a short vowel between two consonants: [cvc]. Shorts and longs syllables oppose each other within short groups, called feet, several of which in turn are linked in metres. Usually a metre occupies a line of verse (or half, being then called hemistiches) ; and verses, rhymed or not, are grouped into stanzas or strophes. Consult Barker (1989), Batmanglij (1988), Crusius, (1951), Erlanger (1949-1964), Gevaert (1965), Guettat (1980), Leech (1991), Nicholson (1994), Sánchez (1995a), Sánchez and Bergé (1997), Sánchez and Puyâ (1996), Shakespeare (1988) and Steingass (1886).
Classical Arabic metres came from the Pre-Islamic times and form the basís of Arabic poetry; they are sixteen in number and can be grouped in circles. Within the same circle we find a syllabic pattern from which each metre is found beginning in different places on the circle. For instance, in the first circle we find the metres Tawil (long), and Basít (simple), whose syllabic patterns are (read from left to right)
Tawil // 4 ¯ ¯ / 4 ¯ ¯ ¯ / 4 ¯ ¯ / 4 ¯ ¯ ¯ //
Basít // ¯ ¯ 4 ¯ / ¯ 4 ¯ / ¯ ¯ 4 ¯/ ¯ 4 ¯ //
which are therefore circularly permuted (we obtain the first beginning in the third syllable of the second); so the name of circle.
Tawil is composed then by four feet, called in Arabic prosody: // fa'ûlun/ mafâ'îlun/ fa'ûlun/ mafâ'îlun //, but suffers usually some changes, as converting the last foot in /mafâ'ilun/, and substituting sometimes the final long of a foot with a short. This is the case in the following example, the first hemistich from a poem by the classical poet Hâtim Tâî, of which we present here its Arabic text, its metric pattern (from right to left) and its syllabification into the meter, in a phonetic transcription according to the IPA:
|
-u9u+yc,Ã\´´¿,^G-²\¯9|«[[x§- v,5¼ÇG/}¯ÇG5¼ÇG-±½,À«[7×É-y·9v«[/ª· |
|||||||||||||
|
¯ |
4 |
¯ |
4 |
¯ |
¯ |
4 |
¯ |
¯ |
¯ |
4 |
¯ |
¯ |
4 |
|
-v |
, |
¼Ç |
/} |
¯Ç |
¼Ç |
-± |
½,Ä«/ |
× |
É- |
-z |
·9v |
v« |
,· |
|
du |
Fa |
/:au |
si |
/am |
/:au |
mu |
li:au |
la |
/:il |
ru |
dah |
l:id |
ha |
If we assign, as we did in Sánchez and Pûyâ (1996), a simple proportion between the durations of shorts and longs, we will find a kind of measured recitation, akin to a musical rhythm. Let us take longs as twice as long as shorts: we find, for the metre Tawil a sequence of musical figures as the one shown in Fig.12: a measure of 24 CP, equivalent to 24 shorts, including a rest of short to complete this simple measure a choice suggested by the necessity of a pause after the line and the shortening of the penultimate syllable both facts may be linked.
Computing its RED in the way defined in the theory above and the appendix, we find the RED of Tawil to be, either 243, if the metre is felt like beginning the 'bar' in the second syllable, or 167, much less, if felt as beginning in the first one: an interesting consequence of our dissonance estimation.
| // 4 ¯ ¯ / 4 ¯ ¯ ¯ / 4 ¯ ¯ / 4 ¯ 4 ¯ // -24-8 -e--\--Q---Q---e---Q---Q---Q---e---Q---Q----e--Q---E---Q--_--e--\ 24 26 28 29 31 33 35 36 38 40 41 43 44 47 -24-8 -\--e--Q---Q---e---Q---Q---Q---e---Q---Q----e--Q---E---Q--_--\ 24 25 27 29 30 32 34 36 37 39 41 42 44 45 |
| Fig.12. Tawîl. RED (R1) = 243. Red (R2)=167. The second one is simpler. |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 ben MÂ i rokh ke BÂGH o go les TÂN a mâ re ZÛST -- // - - 4 - / 4 - 4 4 / - - 4 - / 4 - // |
| Fig. 13 |
The Persian metric system shares with the Arabic the already mentioned 16 classical metres, and adds many others, among which we choose a short example.
| //- - 4 - / 4 - 4 4 / - - 4 - / 4 - // 24-8 -Q -\- Q- -e--Q--e--Q--e--e--Q---Q--e- Q---e--Q--_--_--Q-\ 24 26 27 29 30 32 33 34 36 38 39 41 42 46 |
| Fig.14. |
Let us consider the Persian metre Muzare' Musamman Akhrab Makfuf Mahzuf, whose pattern is // mustaf'ilun/ mufâ'ilu/ mustaf'ilun/ fa'al //, or (from left to right)
; /¯ ¯ 4 ¯ /4 ¯ 4 4 /¯ ¯ 4 ¯ /4 ¯ / according to which this Rûmî's verse is written: Js,cvH Lkhjsg´ , Yhf í; Ov Dhlkf (Nicholson, 1994) that is scanned (from left to right) in Fig.13., and for which we repeat what we did for Tawil, obtaining a different musical pattern within the same measure o periodicity cycle, and, surprisingly, with the same RED than the second form of Tawil.2.2.3. Classical Western metres
They use accentual-syllabic metrics, in which, although syllables are no different in length in the abstract and systematic sense (as speakers and listeners do not perceive quantity differences), but do so at the realization level, assigning slightly longer syllables to accented (stressed) and/or marked (important) syllables in the meter [Sánchez and Bergé,1997].
| q -- ---q ----- q------q -- ---q- ---- q- ----q --- --q-- --- q- ----q -- ---q- ----q---- // 4 - / 4 - / 4 - / 4 - / 4 - / 4 - // 1 2 3 4 5 6 7 8 9 10 11 12 When I do count the clock that tells the time 4 -- we >naI dU >kaunt D_ >kl_k DQt >telz D_ >taim |
| Fig.15. |
Let us choose the Italian endecasílabo with an iambic marking, extended to Spain and many other countries, as England, were it has and still has a tremendous success, with hundreds of continuous lines in this iambic pentameter. We take a fragment of Shakespeare sonnet XII, its first line (Fig.15) as were scanned in Sánchez and Bergé (1998): with longs double than shorts (Fig.16), the resulting measure is not too complicated (RED=83), much less than classical Oriental metres.
| // 4 - /4 - /4 - /4 - /4 - /(4)(-)// 18-8 -e-\--Q--e--Q--e--Q--e--Q--e--Q-(e)-_-e-\ 18 20 21 23 24 26 27 29 30 32 35 |
| Fig.16. |
2.3. Folkloric rhythms: automatic transcription and rhythmic dissonance
Folkloric, traditional popular music presents thousands of rhythms, played, clapped, sung, danced. Since they are often not codified, written, we also often ignore their rhythmic values, i.e., the relative durations between their strokes we do not even know their timbre patterns and repertoire of strokes. See references mentioned in 2.2.
The lack of regular teaching which is often oral and writing leads frequently the musicologist to misunderstand these rhythms, usually by oversimplifying them. Their subtlety is not in their coding but in the actual performance, which happens only in the conscience of players and listeners, both sharing a common culture, especially a musical culture.
To help to attain a better understanding of these performances, we bring some examples, pertaining to two different and primitive musical systems: the Gnâua of Morocco and the Basque Txalaparta (Spain). While in our previous illustrations we have applied a calculation to a written rhythm, taught, and played according to this written code, we dispose only in this case of recorded excerpts, to which we will apply a computer algorithm that extracts the moments of the strokes, the time interval between them their durations, and an evaluation of the approximate ratios between these durations; all this which will give us a rhythmic understanding of the pattern. At this point we can now apply the former calculus to evaluate its RED.
 |
| Fig.17. |
The Gnâua are a spiritual brotherhood with its roots in the south of Morocco; their members are Black and Muslim perhaps with a touch of syncretism. In their musical performance they use a primitive low-toned three-stringed instrument that, with the voice, constitutes the tonal part. Rhythm is represented by pairs of metallic castanets, called kerkbat, each clapped alternately, all percussionists together.
|
s1‑‑s2‑‑‑s3‑‑‑s4‑‑s5‑‑‑s6‑‑s7--s8
144 308 164 406 262 97 524 380 216 118 684 540 375 277 159 842 698 534 436 318 158 952 808 643 546 427 268 109 |
s1‑‑s2‑‑s3‑‑s4‑s5‑‑s6‑s7-s8
3 5 2 7 4 2 10 7 5 3 13 10 8 6 3 15 12 10 8 5 2 |
|
Chronos Protos=54 ms .Quality= 14 |
|
| Fig.18. | |
One of the few patterns that they play is a quick four-stroke one whose temporal structure is not easy to detect, seemingly a cluster of four unmeasured strokes. But a representation of these strokes, shows a very different aspect: they adopt an ordered behaviour with a cycle of four strokes with durations proportional to simple units. An automatic estimation shows a duration pattern of 3-2-2-3 (Fig. 17-18), a surprisingly identical pattern to Jurjûnâ, seen in section 2.1.
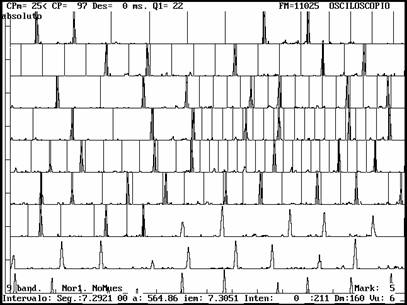 |
| Fig.19. |
2.3.2. Percussion of Basque Txalaparta
The txalaparta is a big wooden bar or plank (around 2 meters), placed on two fixed but flexible
| Cycle of 5 CPs ┬─────────────┬ t k t k t k ┴──┴───┬──┬───┴──┴ 2 3 2 3 2 5 -q- \ ---q -ä-----Q----Q-ä-----q- \ --q Cycle of 20 CPs ┬───────────┬ t k k t k ┴──┴────┬───┴──┴ 4 9 7 4 20 -q -\ ---q--Î -Å----Q- ä-Å---q-- \-- q |
| Fig.20. Two cycles of the traditional toque of txalaparta in Fig.19. Usual musical notation and the one used in Hernani School: stems up, Txakun; down, Herrena. Durations between blows and resultant bars. RED(5-CP) = 17. RED(20-CP) = 38. |
supports, and hit by two players, each one using two small logs to strike alternatively the plank. The strokes of the first player are onomatopoeically called Txa and Kun, a pair regularly repeated, so constituting a turn, cycle or measure. Between these pairs the other player inserts, freely, singles, pairs or other stroke patterns, even nothing at all. The combined playing is perceived as an euphonic and pleasant series of rhythmical phrases, and is called a toque (played performance) of txalaparta. The txalapartaris (players) were musically uneducated and repeated their inherited rhythms without writing them, learned by ear and habit, in festivities related to familiar and agricultural matters.
A superficial listening would probably not find this rhythm rich nor musically interesting. But a similar analysis to what we saw for Ganui percussion, suggests more complex patterns than what could be expected of this rough instrument: in Fig. 19 and 20 we see an evolution from a 7/8 measure to a 10/16 or 5/8, a typical Basque measure, used in the zortzico. The analysis points to an unconscious use of this measure by the players (Sánchez and Beltran, 1998).
By no means do we think to have exhausted the important subject of Rhythmic Dissonance: the added complexity of a timbre pattern, fused with the duration one; the repercussion of tempo in the total complexity slower speed makes rhythm more difficult to grasp; intensity, essential to give expression, life to executed rhythms rhythmopoeia; articulation or variable links between adjacent or contiguous strokes. All these aspects add complexity, interest, beauty to the whole system, while we have considered only one of them, the duration rhythm.
Nevertheless, we hope to have brought a new insight to forgotten this subject, allowing further progresses to be made. In this limited but important domain, the Duration Rhythm indeed the most important, since the cycle periodicity properties and the feelings of repetition, of return, depend on it we think to have accomplished some appreciable steps: a recognition of the necessary harmonious balance between Order and Disorder in Art; an introduction and definition of Duration Rhythm, a definition of Rhythmic Dissonance, for both individual strokes within a rhythm, and for the whole cycle; a definition of 'good' rhythm has been attempted; a distinction between important and filling strokes in a given rhythm has been made; and a method to estimate rational rhythms from actual measurements of time intervals has been presented. These concepts have been applied to Oriental classical rhythms and metres, closely linked, as well as to folkloric recorded patterns.
Thus, despite their incompleteness, these ideas connect again with that ancient and beautiful parallel between Tone and Rhythm the pillars of Music, and therefore link this theory to the prestigious line of thought that considered Number as the basís of Art, even of Nature.
BARKER, A.(ed).(1989) Greek musical Writings,II: Harmonic and Acoustic Theory. Univ. Pres. Cambridge,.
BATMANGLIJ, M. and N. (eds.) (1988). Hâfêz, Dance of Life. Washington: Mage.
CRUSIUS, F. (1951). Iniciación en la Métrica Latina. Barcelona: Bosch.
BACKUS, J. (1977) The Acoustic Foundation of Music. Norton, N.York.
DANIELOU, A. (1959) Traité de Musicologie Comparée. Hermann, Paris.
DURING, J. (1991) Le Repertoire Modele de la Musique Iranienne: Radif. Soroush, Teheran.
ERLANGER, R.D' (1949-1964) La Musique Arabe. Vol.1-6. Geuthner, Paris.
GEVAERT, F.A. ( 1965) Histoire et Théorie de la Musique de l'Antiquité. G.Olms, Hildes.
GUETTAT, M. (1980) La Musique Clasíque du Maghreb. Sindbad, Paris.
HAKKI, I,Ö. (1984) Türk Mûsikîsi Nazariyati ve Usûlleri. Ötüken Ne, Istanbul.
JARGY, S. (1971) La Musique Arabe . Que sais je?. P.U.F., Paris,
Al-KATIB Kitab Kamal Adab Al-Gina (Shiloah, A. ed) La Perfection des Connaissances músicaux. Geuthner, Paris, 1972
KASZIM, A (1964) Terminology of Oriental Music. AlJamhuri, Bagdad.
KARAS, S. (1989) Harmonika:Des consonances par moy.harmoniq. Manoutios. Athène.
KARADENIZ, E. (1965) Turk Mûsikîsinin Nazariye...T.Bank.Y. Ankara.
LEECH, G.N. (1991). A linguistic Guide to English Poetry. London: Longman.
LLOYD, H.B. (1963) Intervals, Scales and Temperament. S.Martin N.York
MALM, W.P. (1985) Culturas musicales del Pacifico, Cercano Oriente y asía. Alianza, Madrid.
MAHDI,S..El (1972). La Musique Arabe. Leduc, Paris.
NICHOLSON, R.A. (1994) Selected Poems from the Divâni Shamsi TabriîzAl Maqam Al-Iraqi. Al-Ma'arif, Bagdad.
RADEMACHER, H. & TOEPLITZ, O. (1970): Números y Figuras. Madrid: Alianza:163
Al-RAJAB, H (1961) Al Maqam Al-Iraqi. Al-Ma'arif, Bagdad.
REINHART, K&U. (1969) Turquie. Les Traditions musicales. Buchet/Ch.Paris.
ROEDERER, J.G. (1979) Introduction to the Physics and Psychoacoustics of Music. Springer, N.York.
SACHS, K. (1966) Musicología Comparada. Eudeba, B.Aires.
SÄNCHEZ. F.J.:
(1985) La Música Culta Arabe Oriental. Coop.Univ.Madrid.