Teorema de Pitágoras
Habiendo surgido el tema con un alumno especialmente díscolo y desconfiado, afirmando que no era posible idear una demostración, me vi obligado a demostrarlo por mi cuenta, llegando a esta, conocida, sí, pero, en fin, alcanzada sin las muletas de la bibliografía.

Está claro que el cuadrado grande horizontal-vertical contiene el interior oblicuo más las cuatro esquinas. Pero el área del primero es (b+c)*(b+c), el del segundo a*a, y el de cada esquina b*c/2. Luego
b2+ c2+ 2bc = a2 + 4(bc/2) = a2 + 2bc luego b2+ c2 = a2
Pero si no nos gusta el uso de números, podemos ver la equivalencia de áreas directamente. Y podemos hacerlo de manera sencilla, con sólo 5 piezas:
Nótese que, en el triángulo rectángulo a-b-c:,
construimos un cuadrado con lado b+c. A continuación se construye el
cuadrado sobre b, y sobre la línea superior se coloca el cuadrado sobre c, a
su derecha. Además construimos sobre la hipotenusa su cuadrado, y desde su vértice
superior, la perpendicular a la citada línea formada por los dos lados
superiores de los cuadrados sobre b y c. Las piezas que aparecen reciben
nombres similares cuando son iguales: así ocurre con el los triángulos D y D'
de altura c, y con E y E' de altura b-c. Y con B y B de altura c y base b.
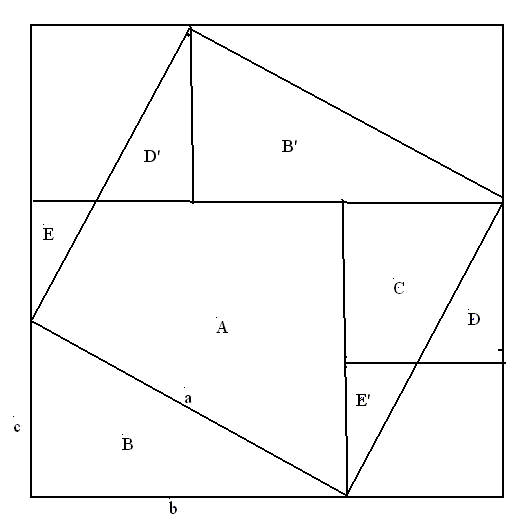
En la figura se cumple:
b^2 = B+A+E, y c^2 = C+D. Pero como a^2=A+D'+B'+C+E',
resulta que en efecto: a^2 = b^2 + c^2; de modo que en efecto:
el cuadrado de la hipotenusa de un triangulo rectángulo es igual a la suma de los cuadrados de los catetos.
Recórtense las piezas, como yo hice, y se verá la perfecta equivalencia. Además la igualdad de las formas y áreas de las piezas correlativas (letras con y sin prima) se ve acompañada por una igual posición, no hay que girar ni reflejar, sólo trasladar.
Incluso ¿puede hacerse con sólo 4 piezas?
Pues sí, ya que las aquí llamadas A y C pueden formar una sola.
También pudieran haberse considerado los cuadrados menores a la izquierda de la figura, quedando también a la izquierda los tres polígonos a trasladar, con idéntico resultado.
¿Y pueden usarse sólo 3 piezas?. Dejamos el intento a mentes curiosas.
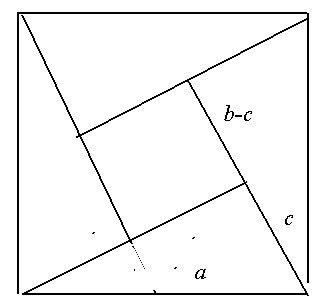
Otra demostración, más aritmética, es la que equipara a^2 = c^2+4(b-c)c/2), por simple inspección de la figura central y cuatro triángulos como el dado que completan el gran cuadrado.
 |
 |
| Otra demostración del Teorema y lacería en Isfahan (Iran) | |
Curiosamente, hemos encontrado un patrón parecido, sin duda consciente de su enlace matemático, en una lacería cerámica en Isfahan (Irán). La traemos aquí.
Vuelta al Principio Última
actualización:
Sunday, 28 de July de 2013
Visitantes: