Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
Proporción de plata
Generalizando la proporción dorada, introducimos (sin conocerlo anteriormente):
El número q
Lo definimos como
√17 - 1 q = -------- 4
resultando su valor: q = .78077406...
Este número se comporta de manera parecida en su álgebra al número de oro, F. Después examinaremos sus propiedades geométricas.
Veamos su perpetuación en sus potencias. En efecto el cuadrado de q da:
(√17 - 1) (√17 - 1) / 4.4 = (17 + 1 - 2√17 ) / 4.4 = (16 + (2 - 2√17) ) / 4.4 = 1 - ( (√17 - 1) / 4 ) / 2 = 1- q / 2
De modo que:
q 2 = 1 - q / 2
Continuando con el cubo:
q 3 = q ( 1 - q / 2) = q - q 2 /2 = q - (1 -q / 2) / 2 = 5 / 4 q - 1/ 2
la cuarta potencia:
q 4 = q 2 .q 2 = (1 - q / 2 )2 = 1 - q + q2 / 4 = 1 - q + 1/4 - q / 8 = 5/4 - 9/ 8 q
y así, sucesivamente, encontramos una sucesión de potencias.
Por otra parte, su inverso:
q -1 = 4 / (√17 - 1) = 4 (√17 + 1) /[ (√17 - 1)(√17 + 1) ] = 4(√17 + 1 ) / (17-1) = (√17 + 1 ) / 4
q -1 = (√17 + 1 ) / 4
expresión simétrica, de comportamiento similar a F. En función de q, q -1 vale:
q -1 = (√17 + 1 ) / 4 = (√17 + 1 ) / 4 = (√17 - 1 + 2 ) / 4 = q + 1/2
De modo que:
q -1 = q + 1/2
y
q -2 = (q -1) 2 = (q + 1/2) 2 = q 2 + q + 1/4 = 1 - q / 2 + q + 1/4 = q / 2 + 5/4
con lo que obtenemos la tabla (redondeando valores)
| Potencias de q | Coeficientes de | Valor | Sucesión de | |
| 1 | q | |||
| ... | ... | .... | .... | .. |
| -8 | ||||
| -7 | 129/128 | 65/64 | 65/64 | |
| -6 | 65/64 | 33/32 | 4.4141... | 33/32 |
| -5 | 33/32 | 17/16 | 3.4464... | 17/16 |
| -4 | 17/16 | 9/8 | 2.6908... | 9/8 |
| -3 | 9/8 | 5/4 | 2.1010... | 5/4 |
| -2 | 5/4 | 1/2 | 1.6403... | 1/2 |
| -1 | 1/2 | 1 | 1.2808... | 1/1 |
| 0 | 1 | 0 | 1.000... | -- |
| 1 | 0 | 1 | .7808... | 1/1 |
| 2 | 1 | -1/2 | .6096... | 1/2 |
| 3 | -1/2 | 5/4 | 4760... | 5/4 |
| 4 | 5 /4 | -9/8 | .3716... | 9/8 |
| 5 | -9/8 | 17/16 | .2902... | 17/16 |
| 6 | 17/16 | -33/32 | .2265... | 33/32 |
| 7 | -33/32 | 65/64 | .1770... | 65/64 |
| 8 | 65/64 | -129/128 | ||
| ... | ... | .... | .... | ... |
El término general es, evidentemente (se genera operando en las potencias sucesivas):
Qn = (-1) n-1 . (1+2(n-2)) /2 (n-2) + (-1) n . (1+2(n-1)) /2 (n-1) q
Qn = (-1) n-1 . (1 + 2 - (n-2) - (1+2 - (n-1)) q
Qn = (-1) n-1 . (1 - q - 2 - (n-2) (1- q /2)
expresión que comprobamos aplicándola para n=10, operando directamente con el valor de q:
Q10 = - ( 1+2 - 8 - q (1+2 -512) = - 129 / 256 + 257) /512 q = .08419otra vez comparamos con la tabla, n=7: +++++++++
Q10 = ( 1 - 2 - 8 - q (1+2 -512) = - 129 / 256 + 257) /512 q = +++++
(comprobar otra vez)
Construcción geométrica
La realizamos sencillamente, como hicimos para F
, construyendo un triángulo
rectángulo de catetos en proporción 1 a 4. La hipotenusa AB mide por lo
tanto √17,
a quien restamos 1 llevando el cateto vertical sobre ella mediante el
compás; así, BC = √17
-1.
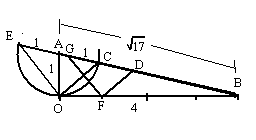
Para dividir por 4, establecemos una semejanza entre el cateto horizontal, OB, que mide 4 y BC, uniendo C con O y trazando una paralela por el punto F, a distancia 1 de O (siempre posible porque trazamos OB al principio con cuatro unidades iguales arbitrarias).
Como 1/4 = OF/OB = CD/CB, entonces
CD = CB/4 = (√17 - 1) / 4 = q
y, de manera similar:
Trigonometría
Como valor trigonométrico corresponde a los ángulos:
| .7808.. | razón | seno | coseno | tangente |
| .arco | 51.34..º | 38.66º | 38º | |
donde como única novedad se aprecia la cercanía de los valores de los arco coseno y tangente
Proporción visual
Representamos como rectángulos apaisado y vertical, como cuadros. que también (como la dorada) son agradables.
|
|
|
|
Connotación musical
Los elementos de la sucesión en la última columna de la tabla (a partir de valor 3, a ambos lados del centro) representan los intervalos entre las octavas y el harmónico superior, que corresponden sucesivamente al unísono, la tercera mayor, el semitono natural es decir, presente en la serie harmónica..... Véalos en La espiral harmónica.
El tamaño de q considerado como intervalo es de algo más 4 semitonos, 428 cents, tercera mayor alta, pues. Su complemento a la octava es una sexta menor baja.
Registramos estos hechos sin más comentarios a la espera del encuentro con algún sentido suplementario, propio o procedente de algún lector listo y benévolo.
Vuelta al Principio Última
actualización:
Sunday, 28 de July de 2013 Visitantes: