NEY TURCO

Se representa  un Ney de forma semirrealista.

Vamos a modelizar la compleja relación entre agujeros abiertos y cerrados según los siguientes convenios:

1. La longitud efectiva L' (aquella según la cual se calcula sencillamente la frecuencia emitida) es función de la longitud real L, el diámetro interior del tubo d --supuesto cilíndrico-- de acuerdo con la fórmula empírica

    L'  =  L + pD  (revisar)

es decir, más grave cuanto más grueso. Un valor usual para p es .58

2. Cada agujero que abrimos más arriba (cercano a boquilla, acorta el tubo efectivo) que otro afectará a la distancia efectiva generada por él, con lo que las acciones de todos los agujeros se suman en una sucesión de acortamientos sucesivos.

Puesto que un agujero muy pequeño no acorta apenas el tubo, y uno muy grande lo corta prácticamente, solo nos resta hallar la longitud efectiva l' en función del diámetro orificial d: una función que pasa por los puntos (0, L)  y  (1, a) y , según se representa en la figura

                                                a' = L' - f(x) . b

Adoptemos una función simple, la lineal primeramente. f(x) = x, o bien cualquier otra potencia de x,  xⁿ , ya que todas valen 0 para x=0 y 1 para x=1.

3. Por lo tanto, la longitud efectiva L' para un agujero abierto, depende de su posición en el tubo, medida por su distancia al extremo superior a, donde se emite el aire, y su diámetro d

         a' = a * d/D +  L' (1-d/D) = L' - (L'-a) d/D =  L' - b' . x 

lo cual aplicamos a la longitud iniial, agujero 0 de diámetro máximo, x=1, siendo

          L = a_o ,           d_i / D  =  x_i           b_o' = (a_o'- a₁)        a₀'  =   a + D

  a' = a * d/D +  L' (1-d/D) = L' - (L'-a) d/D =  L' - b' . x 

es decir que la relación x = d/D , que varía de 0 a 1, es un factor para la distancia del agujero al extremo inferior, que se resta a la longitud real: todo si el agujero es muy grande, nada si es muy pequeño, como confirma la práctica.

           a₀'  =  a_o + t (D)   

             a₁'  =  a_o' - b₁' . x_{1  =}  a_o' - ( a_o ' - a₁ ) . x_{1   =}  a_o' - ( a_o + t (D)   - a₁ ) . x_{1 =}

                            ₌  a_o' - ( a_o + t (D)   - a₁ ) . x_{1 =}

                             ₌  a_o' -  a_o'  . x₁ - a₁  . x_{1 =}

                          ₌  a_o' -  a_o'  . x₁ - a₁  . x_{1  =}

                        ₌  a_o' ( 1 -  x₁ )  - a₁  . x₁    = ( a_o' + a₁ )( 1 -  x₁ )  -  a₁  =  

     a₁'   = ( a_o' + a₁ )( 1 -  x₁ )  -  a₁    

     a₂'   = ( a₁' + a₂ )( 1 -  x₂ )  -  a₂    =

             ((  ( a_o' + a₁ )( 1 -  x₁ )  -  a₁   ) + a₂ )( 1 -  x₂ )  -  a₂    =

            =  (  ( a_o' + a₁ )( 1 -  x₁ ) -  a₁   +  (a₂  )( 1 -  x₂ )  -  a₂    = 

             =   (  ( a_o' + a₁ + a₂ )( 1 -  x₁ )( 1 -  x₂ )  -  a₁   + a₂  ) - a₂   

             =   ( a_o + t (D) ) . ( 1 -  x₁ )  - a₁  . x₁      

      a₂'   =  a₁' - b₂' . x₂    = a_o' - b₁' . x₁ - b₂' . x₂ 

     

     a'_n = S_j  (a_j x_j P_i (1+x_i ) )       donde          0 <= j <= n,   j < i <= n,

     

      a1'  =   L' - (L'-a1) d1/D = a0' - (a0'-a1) x1,    siendo L = a0   y     di/D = xi.

      a2'   =  a1' - (a2-a1') x2 = a1' (1+x2) - a2x2 =

                    = (a0'- (a0'-a1 ) x₁ ) (1+x2) - a2x2 =

                   = (a0' (1+x1)-a1x1)(1+x2)-a2x2=

                   =  a0'(1+x1)(1+x2)+a1 x1(1+x2)+a2x2 =

                   = a0 . x0 (1+x1) (1+x2) + a1. x1 (1+x2 ) + a2 .x2

y así sucesivamente, para nuevos agujeros abiertos.

es decir cada longitud real del tubo con un agujero abierto se ve afectada por factores que dependen del propio agujero y de todas los anteriores abiertos, como la práctica confirma cuando los agujeros son suficientemente estrechos (como en la flauta de pico). Por lo tanto

a'_n = S_j  (a_j x_j P_i (1+x_i ) )       donde          0 <= j <= n,   j < i <= n,

Esta bella fórmula, que juzgamos al menos verosímil, ha de ser verificada empíricamente, de modo que su simulación conducirá a representaciones de flautas reales si constituye un buen modelo.

Así será implementada en la forma llamada Ney de Mapatone.

Para un flauta con agujeros equidistantes de diámetro mitad del tubo, la ley será

                                              a₁= a₀ -  b₁ / 2

Conicidad del tubo

Veamos en detalle, siempre con nuestra perspectiva naif, esto del tubo cónico.

Podemos suponer que la propagación de una perturbación a lo largo de un tubo depende de su sección, ya que la velocidad del aire así lo hace. ¿Lo hace?. Si el movimiento es continuo es cierto, por Bernouilli. Puesto que la perturbación es un desplazamiento podemos suponer que así ocurre con la perturbación, ese movimiento local que comprime las capas adyacentes y que por lo tanto , por elasticidad hacen lo propio con las siguientes: eso es una perturbación, un mensaje que corre de boca en boca.

Empíricamente lo comprobamos en un nai, cuyo tubo cónico presenta entre otros un agujero hacia el medio: ñpiues bien haciendo sonar ambas mitades, resulta el tono alen el extremo ancho, un semitono aproximado más bajo que en el estrecho.

Es decir, que por ir más despacio en la parte ancha, como suponémos, tarda más en ir y venir, es decir, en vibrar una vez establecido el régiemn permanente de idas y venidas en el tubo: la frecuencia es pues menor, ya que el periodo es mayor.

Es decir que un agujero en tubo ancho corresponde a una situación más alejada en tubo cilíndrico: e el nai, cuya extremo de soplo es el ancho, esto quiere decir que los agujeros corresponden  a otros más cerca del otro extremo, el estrecho, si el tubo fuera cilíndrico.

asimismo, los diámetros son menores en comparación a la sección, más ancha, lo que indica que acortan el tubo menos. y que producen un sonido más bajo.

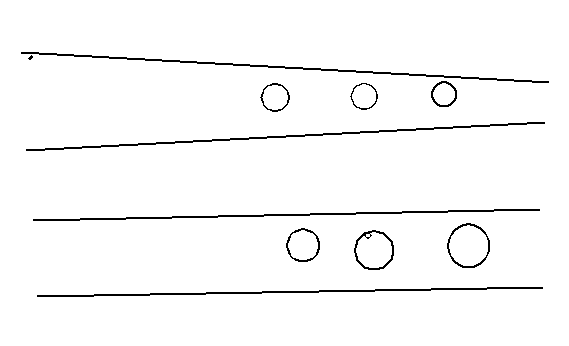En resumen, la conicidad del tubo combinada con agujeros de sección igual produce sonidos mas graves que los que corresponderían a uu tubo cilíndrico con igual longitud y situación similar. (y un diámetro de agujero que tomaremos como medio, por ahora).

Si representamos el tubo cilíndrico equivalente nos encontraremos con agujeros más alejados del extremo de soplo, y de diámetros crecientes al alejarse de él. Estos procesos son dependientes

tran