sta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
EL MAPA de las VECINDADES entre NOTAS, MODOS y TONOS
INTRODUCCIÓN
Abordar el complejísimo y rico mundo de la harmonía mediante unos pocos principios basados en la consonancia (pues ese es nuestro propósito), parecerá quizá arriesgado al músico compositor e incluso al teórico de la harmonía.
Pero, de igual modo que unos pocos principios estéticos dan lugar a un estilo, o que unos principios formales dan lugar a una apariencia (como los árboles presentados en nuestro prólogo), es nuestra intención unificar la harmonía, o las harmonías, en unos principios qu cubran, sin detalles, claro está, las tendencias que han predominado a la hora de hacer sonar varios sonidos (con tono) simultáneos.
Nos alejamos radicalmente, pues, de un tratamiento histórico, que mostraría las infinitas gradaciones con que fueron imponiéndode soluciones a acordes y enlaces. Y por otra parte, de una revista o catálogo de acordes u cadencias posibles: no tenemos esa capacidad, ni es nuestro propósito. Menos aún se trata de un tratado de harmonía de los que ya hay numerosos y algunos excelentes ejemplos (ver referencias)
Prolongaremos pues las nociones introducidas en anteriores capítulos e intentaremos aplicarlas a una descripción unificada (no explicación, concepto vacío en su significado profundo) de aquellos principios. Y pedimos a los lectores de estas líneas que comprueben su vigencia y coincidencia con su experiencia musical, asíntiendo o protestando vigorosamente, según el caso.
|
|
INTERVALOS NATURALES
Volvamos a la serie harmónica representada en nuestra Espiral Harmónica El primero y segundo harmónicos están muy emparentados entre sí en la percepción: son 'el mismo' en cuanto que dos melodías separadas por ese intervalo suenan 'igual' y son empleadas de manera quizá espontánea por hombre y mujer cantando juntos (a veces emplean la quinta, que ahora veremos).
Inmediatamente se perciben como vecinos al fundamental el tercer harmónico, razón 3/1, y su octava inferior, llamada quinta ( razón 3/2); entre el tercero y cuarto harmónicos existe el intervalo 4/3, llamada cuarta, etc. Todos los harmónicos contíguos forman entre sí razones de la forma (n+1)/n, intevalos que recibieron el nombre de supernumerarios.
Todos estos intervalos de producen, como se ve, en la vibración natural de algunos cuerpos, por ello los llamaremos naturales. Sin embargo no dejamos de reconocer que en la naturaleza se producen otros intervalos muy diferentes, entre los parciales de un cuerpo vibratorio, como en todos los cuerpos de dos o tres dimensiones (membranas, placas, campanas, etc.) o incluso de una, como en el caso de barras finas y rígidas. Dejaremos para más adelante la consideración de intervalos entre estos parciales no harmónicos) y nos centraremos en los parciales harmónicos, base de la inmensa mayoría de la música que conocemos en los tres últimos milenios.
La importancia de estos intervalos naturales reside pues más en la sencillez perceptiva o consonancia, que en su naturalidad física. La música griega los empleó, y la oriental, árabe, turca, bizantina, india) todavía lo hace, aunque el contacto con la cultura occidental tuende a socavar esa preservación. La música occidental, tempearndo, parece haberlos abandonado. Pero solamante lo finge: cuando hay ocasión vuelve a ellos; y todo el sistema harmónico, conquista occidental hunde sus raices en aquellas relaciones primordiales.
CONSONANCIA Y DISONANCIA.
La consonancia y su opuesta (la disonancia) son sensaciones de la más alta influencia en lo musical, pues han dado lugar al juego de tensiones y distensiones en lo tonal que han producido melodía, escalas, modos y harmonía.
Aunque abarca varias sensaciones vecinas (agrado, fusión, suavidad, harmonía) la tomaremos en sentido de Pureza-Simplicidad o Riqueza-Mezcla: los tonos consonantes entre sí se mezclan y dan lugar a un timbre simple, fácil de percibir, sencillo. No diremos agradable, pues ello implica una preferencia: y ya sabemos que de la alternancia entre consonancia y disonancia nace la música: no pueden existir una sin la otra.
HIPÓTESIS SOBRE PERCEPCIÓN DE LA CONSONANCIA
Veamos unas hipótesis sobre nuestra percepción en relación con este tema.
PH0. La percepción extrae de un sonido periódico una sensación llamada Tono (pitch): y de una combinación (audición simultánea) de tonos, una impresión llamada Consonancia (Disonancia). Estos son hechos naturales. La Cultura y la Educación modifican sólo su valoración (pueden ser encontrados agradables o desagradables).
La consonancia tiene su origen en una actividad neurológica. La educación puede enseñar a reconocer y usar este fenómeno perceptivo de una manera musical y artística, incluso rechazandole, evitando consonancias fáciles.
PH1. Percibimos un intervalo, y su consonancia, como la más simple y más cercana de las consonancias compatibles con el código musical del oyente.
Queremos decir con esto, que en un universo diatónico, esperamos y forzamos las notas que oímos, a pertenecer a ese universo. Si cambiamos a un universo cromático, tendremos más códigos, más categorías en que clasificar los sonidos que oímos. Si ampliamos a un universo microtonal, percibiremos como significativos e independientes lo que eran sólo variedades y matices en los más simples universos anteriores.
Este forzar la afinación de un sonido para que encaje en nuestro código musical no implica que lo percibamos como correcto: simplemente carecemos de código especial para él, con lo que simplemente 'no existe', y es asímilado a otro vecino. Esto nos permite reconocer música interpretada por instrumentos desafinados.
Una cómoda prueba: una escala temperada de 5 intervalos iguales por octava será probablemente percibida inicialmente como una pentatónica del tipo do-mib-fa-sol-sib-do. Nuestro código usual, la temperada de 12 semitonos por octava, fuerza a estos sonidos a entrar en él.
Este efecto permite la enharmonía, por ejemplo, donde un tono único es percibido como formando consonancias con diferentes grupos de tonos (acordes); o sea, else tono es perceptivamernte modificado para consonar con ambos grupos.
PH2. Cualquier intervalo tiene un Tamaño perceptivo que crece contínuamente al crecer el intervalo. Tiene también un Color, un Carácter, que cambia a saltos repentinos, de acuerdo con los números primos involucrados en la relación de sus frecuencias.
Los nombres dados a algunas notas o grados de la tonalidad (sensible, dominante) apuntan a ese 'color'. La percepción oriental de esos colores ha sido tradicionalmente más aguda y fina. Por ejemplo los nombres indios de los shruti (microintervalos) muestran ese carácter; como se ve en Danielou []:para dos correspondientes a nuestra tercera mayor:
natural 5:4 do.mi- Prasârini es difusa, penetrante, tímida, suave, reposante
pitagórica 81:64 do.mi Pritih es energica, sensual, jubilosa, sugiere placer, amor, delicia.
Por supuesto, ese color puede ser percibido y usado sólo después de un entrenamiento adecuado; pero está ahí. Mediante PH1 puede (hasta cierto punto) ser simulado por otros intervalos vecinos, como se hace con la escala temperada; pero creemos que perdiendose así gran parte de su efecto expresivo y emotivo.
Empleamos el término 'color' para conservar una acepción vecina a 'timbre'; en efecto, hay una especie de timbre característico en la tercera menor, diferente de la quinta o el tritono. Este color es fundamental en el carácter de los acordes, los cuales tienen una especie de individualidad en su carácter.
Para resumir este punto, relacionándolo con el Número, diremos que cada intervalo tiene un tamaño y un color: su tamaño depende de su cardinal (medida entera); su color de su estructura de divisibilidad.
PH3. Cuanto más tiempo oímos un intervalo, mejor percibimos su tamaño, su consonancia y su color.
A medida que aumentamos la densidad de grados (disminuímos el intervalo entre grados contíguos), nuestro mecanismo analizador necesita más tiempo para discriminar entre ellos, como culaquier otro mecanismo (tipo Fourier u no); ello es debido a una imprecisión inherente a todo análisis frecuencial, no a defectos del mecanismo.
Esto querría decir que, de acuerdo con PH1, podemos reconocer música pentatónica rápida, pero necesitamos que la microtónica sea lenta: de otro modo oiremos probablemente algo así como clusters o glissandos cuando hay intervalos microtónicos vecinos, o, si son disjuntos, los asímilaremos a otros más consonantes; por ejemplo, 720 (702+20) cents serán percibidos como una quinta si es breve su duración, incluso en un ambiente en que el intervalo de 28 cents pertenezca al código.
Todo esto parece ser responsable del más fijo y exacto tamaño que exigen las consonancias más simples (octava, quinta) respecto a los tamaños más variables y flexibles de las consonancias más complejas ( semitonos moviles, pien, grados variables, etc.)
PH4. Todo juicio perceptivo sobre consonancia se hace sobre las últimas notas oídas hasta el momento.
Esto quiere decir que atribuímos una medida subjetiva de la consonancia a un cluster compuesto por los últimos sonidos, incluso aquellos que ya han desaparecido: se mantienen en la menoria cercana, y probablemente decaen en su importancia a medida que nuevos sonidos les reemplazan.
El caso más simple es el de dos notas sucesivas: inevitablemente se percibe la relación de consonancia de la segunda respecto a la primera: la memoria convierte un arpegio en un acorde.
Un importante colorario es:
PH5. Cualquier medida de la consonancia debe incluir la nota de referencia (tónica, finalis, tonica modal, etc) si la música anteriormente oída la sugiere (música tonal, modal, etc).
En estos tipos de música, la consonancia actúa durante toda la pieza: por ejemplo en instrumentos de cuerda, afinándolas en fuertes consonancias como quintas , cuartas y octavas. después, durante la interpretación, buscando las consonancias en ensayos repetidos en instrumentos de afinación variable, como violín.
En música modal, la elección de determinadas consonancias entre los grados (lo que implica rechazar otras) fija las notas principales del modo; su estructura y jerarquías se construyen de esta manera (véanse las hipótesis M en A.6.5).
TEORÍA DE LA CONSONANCIA DE EULER
El gran matemático Euler se interesó (entre muchos otras temas) por el problema de la consonancia y elaboró una interesante teoría basada en la descomposición en factores primos de los números que expresan las relaciones de frecuencia de los sonidos entre sí.
Si un número natural A es expresado como producto de primos, Euler define su grado de complejidad C(A), como
| i i A = P pi ai entonces: EC(A) = 1 + S ai (pi-1) |
siendo pi (p sub i) los factores primos de A, ai (a sub i) sus exponentes, y
A y E los signos de producto y sumatorio. Por ejemplo la complejidad de 8 (2 al cubo ) es 1+3.(2-1)=4 mientras que la de 9 es 1+2(3-1)=5; es decir 8 es más sencillo que 9.El grado (de disonancia) de un intervalo reducido a números mínimos es simplemente el grado del producto de numerador y denominador. Así, la quinta 3/2 tiene el grado 4, el de 6 (1+2+1), la cuarta 4/3 tiene 5 (1+2+2), etc.
En general el grado de disonancia de un conjunto de notas, como un acorde, vendra dado por la complejidad del cociente entre el mínimo común múltiplo y el máximo común divisor de sus frecuencias:
| / m.c.m (a,b,c,.) \ Dis (a,b,c,..) = EC (----------------------) \ m.c.d(a,b,c,.) / |
Por ejemplo, las frecuencias 220,330,440, la-mi-la, tienen una disonancia como acorde igual al grado de disonancia del cociente (3×4×110)/110 = 12, que es 1+2×(2-1)+1×(3-1) = 5; y lo mismo los acordes do-sol-do o mi-si-mi. El acorde mayor en su forma fundamental, como do-mi-sol, reducido a cifras sencillas, tendrá siempre unas frecuencias proporcionales a 4-5-6, lo que nos lleva a una disonancia igual a la complejidad de 60, que es 9, mientras que el menor, la-do-mi, proporcional a 5/6-1-5/4, o sea, 10-12-15, tiene un grado como el de 60, otra vez 9.
Otras inversiones de un acorde pueden variar la disonancia: por ejemplo, el caso sol-do-mi, proporcional a 3/4-1-5/4, o 3-4-5, da 9, como antes (a partir de 60) pero mi-sol-do, 5/4-3/2-2, o 5-6-8, da 10 (el de 120, 1+3+2+4 = 10).
La teoría de Euler parece coincidir bastante bien con el sentimiento común del músico, y por otra parte ofrece una medida de una cualidad aparentemente tan elusiva al número como la consonancia. Es una interesante teoría, y más aún por su sencillez.
Es posible encontrar una relación entre esta estimación de esta consonancia aparentemente sólo aritmética, y la percepción basada en la neurofisiología. En efecto, un sonido con tono tiene una frecuencia de repetición de una forma de onda, cuya duración es un período. La audición simultánea de dos sonidos de períodos primos entre si creará una forma de onda cuyo período será el producto de aquellos; es decir habrá un tiempo de concepción simultánea, el período de la onda, tanto mayor cuanto más complicada es la relación entre esos primos. Y la complicación y disonancia sera tanto mayor cuantos más sonidos primos añadamos. En el siguiente párrafo desarrollamos estas ideas.
El caso es idéntico, pero en escala temporal mucho menor, al de un ritmo, tanto más difícil de comprender y concebir, cuantos más golpes (irreductibles) contenga.
Helmholtz extendió esta relación basada en las frecuencias fundamentales de los tonos de varios sonidos a sus harmónicos. Ahora la complejidad se dá entre los componentes de las familias de harmónicos de cada sonido, complicándose la cosa; no obstante, él trata el tema en el dominio de las frecuencias, considerando los batidos o chirridos que harmónicos de frecuencia vecina producen en el oído.
En el cuadro contiguo pueden verse las disonancias según Euler de los principales intervalos supernumerarios que forman la base perceptiva de nuestras escalas. Se incluyen otros datos a los que volveremos más tarde.
El lector juzgará si estos números corresponden a su estimación, recordando, eso sí, que su práctica musical ha influído en su valoración natural o primitiva.
EL ESPACIO EP. ESPACIO VECTORIAL DE LOS INTERVALOS
Ya vimos en el cap.00 que todo numero natural puede ser descompuesto en factores primos, en la forma:
|
i i Si A = A pi ai entonces: EC(A) = 1 + E ai@(pi-1)
|
|
N
0)0 a A = * * p 6 1
|
donde 'pn' son los primos 2,3,5,7,.., 'an' los exponentes de esos primos en el número, y N es el signo de infinito. Los primos son , ordenadamente:
|
p1 p2 p3 p4 p5 p6 p7 p8 |
| 2 3 4 7 11 13 17 19 ... |
El uno no se suele considerar primo, o bien un primo trivial, siempre presente; nosotros lo desechamos como primo; admite una n-upla en función de los demás:
0 = { 0 0 0 0 0 0 ... }
y las n-uplas que representan los números 1, 2 ,3, 180 son:
1 = { 0 0 0 0 0 0 ... }
2 = { 1 0 0 0 0 0 ... }
3 = { 0 1 0 0 0 0 ... }
180 = { 2 2 1 0 0 0 ... }
Podemos además representar así, no solo los naturales, sino también todo numero racional (cociente de naturales ); en este caso algunos de los exponentes serán negativos (denominador) y otros positivos (numerador). El número 9/8 = 3^2 / 2^3 = 2^(-3)
@ 3^2. o sea 9/8 ={ -3 2 0 ... }. Otros ejemplos:3/2 = { -1 +1 0 ... }
4/3 = { +2 -1 0 ... }
32/27= { +5 -3 0 ... }
En general:
A = { a1 a2 a3 a4 a5 }
sobreentendiéndose en este caso que los exponentes superiores al último representado son nulos, siendo los demás positivos, nulos o negativos, es decir números enteros. Llamamos como antes 'A', al Número y 'a' ,su n-upla o vector (ahora lo demostraremos) asociado.
Los productos y cocientes de números quedan también representados, pasando a ser suma o diferencia, elemento a elemento de las núplas correspondientes:
@ 4 = ( 2 @ 5 ) @ ( 2 @ 2 ) = ( 2^1 @ 5^1 ) @ ( 2^2 ) = { 1 0 1 .. } + { 2 0 0 .. } =10
= { 3 0 1 .. } = 40
(10/9)*(9/8) = { 1 -2 1..} + { -3 2 0 .} = { -2 0 1..} = 5/4
y la potencia entera:
(3/2)^3 = { -1 1 0 ..} + { -1 1 0 ..} + { -1 1 0 ..} = 3
@ { -1 1 0 ... } = { -3 3 0 ... } = 27/8Estas n-uplas constituyen un Espacio Vectorial, como vamos a mostrar. En efecto, se cumplen las condiciones de espacio vectorial (véase el párrafo 00l, capítulo 00) con las operaciones de suma de vectores y producto de vector por número real, que corresponden en aritmética, al producto de números y la potencia de un número.
a + b = { a1 a2 a3 a4 a5 } + { b1 b2 b3 } = { a1+b1 a2+b2 a3+b3 a4+0 a5+0 }
N 0)0 ( a + b )
=
* * p 6 6 = A . B 61
con las propiedades adecuadas de la suma (conmutativa, asociativa, distributiva).
asimismo se ve facilmente que que
".a = B , multiplicar los elementos del vector por un número, entero o real, equivale a hallar la potencia de número correspondiente al vector A:
".a = " @ { a1 a2 a3 a4 a5 } = "@a1 "@a2 "@a3 "@a4 "@a5 } = N N 0)0 "@ a / 0)0 a \ " "B =
=
* * p 6 = ( * * p 6 ) = A1
6 \ 1 6 /con todas las propiedades de ese producto (distributiva, asociativa).
Existe además en Vector Nulo o Neutro (n-upla nula) y el vector opuesto de cualquiera, es cual sumado con el da el nulo (n-upla con valores de signo opuesto).
El conjunto de todas las n-uplas con componentes (los exponentes) enteros es un Espacio Vectorial respecto a las operaciones citadas; le llamaremos EP, espacio primal de los números racionales positivos, es decir, de los intervalos.
Ya se ve, y esta es la razón de su introducción, que este espacio nos sirve admirablemente para representar intervalos y operaciones con ellos. Posee además otras propiedades que ahora veremos. Representemos algunos intervalos en el subespacio de tres dimensiones correspondientes a los primos 2, 3, 5. ( véanse figuras adjuntas)
SUBESPACIOS EN EP
Puesto que no todos los fraccionarios están formados por todos los primos, podemos considerar únicamente los formados por un número limitado de ellos. Por ejemplo, considerando todos los quebrados cuyos términos contengan sólo 2 y 3 como factores primos, todos ellos pueden encontrarse combinando 2 y 3 adecuadamente. Así, 9 = 3
@3, o sea (0,2,0,0,..), y 81/64 será (-6,4,0,0,0,...).Es claro que ninguna combinación de estos vectores hará aparecer un no nulo en componentes superiores a la segunda. Así que este conjunto de números fraccionarios citados constituyen a su vez un espacio vectorial completo; pero al que llamamos Subespacio EP2 por estar contenido en el espacio más general EP y contar con todas sus componentes nulas excepto las dos primeras. Prescindimos pues de las demás y representamos simplemente los vectores con 2 coordenadas. 9 = (0,2), y 256/247 = (8,4) .
Ya veremos ( lo vemos ya) que las escalas pitagóricas están contenidas por completo en el espacio EP2, mientras que las naturales de Zarlino lo hacen en el EP3. Es muy interesante inquirir por qué no se han desarrollado escalas en espacios mayores, es decir, con más primos.
REPRESENTACIÓN EN EP Y PARALELISMO CON LOS CONCEPTOS musicalES
Todo el sistema interválico y escalar tiene aquí su representación adecuada.
Adoptada una frecuencia de base, que tomamos como referencia, como fundamental en la representación y que corresponde al 1, origen de coordenadas (n-upla nula), cualquier otra frecuencia relacionada con ella mediante intervalos naturales aparecerá como otro punto del espacio EP; el intervalo que 'lleva' una a la otra será el vector que les une, con origen en la frecuencia de partida, y punta en la de llegada. Un nuevo intervalo sobre esta última frecuencia nos lleva a otro punto, y así sucesivamente. El intervalo es entonces un vector del tipo llamado libre, que puede trasladarse paralelamente a sí mismo sin dejar de ser él mismo.
Adoptemos una frecuencia de referencia cualquiera, 64 hz., por ejemplo, y elijamos movernos en el subespacio EP2 ( que emplea sólo los 2 primeros primos, 2 y 3).
El salto de tono pitagórico ascendente, 9/8, nos lleva desde punto origen (0,0) (64 hz) al punto (-3,2) correspondiente a 72 hz, mediante el intervalo-vector (-3,2). El paso a un nuevo tono ascendente nos lleva a 81 hz (64
@9/8@9/8), al que corresponde el punto (-6,4), mediante el mismo vector libre (-3,2). Vectorialmente:(-3,2) + (-3,2) = (-6,4)
o bién (figuras adjuntas):
@(-3,2) = (-6,4)2
Conceptos bien conocidos en los espacios vectoriales quedan perfectamente reflejados en nuestro espacio EP. La base del espacio, el conjunto de vectores que pueden engendrar todo el espacio, es uno de los más fecundos. Hasta ahora hemos utilizado la base natural, compuesta por vectores ligados a un solo primo, cada uno.
El cambio de base nos simplifica la comprensión y representación de este universo interválico, mediante la elección de una base adecuada a la escala utilizada. Por ejemplo, en la escala pitagórica, de la que ya sabemos, aunque se verá mejor en el capítulo 3, que consta sobre todo de tonos 9/8, será cómodo utilizar precisamente ese intervalo como vector de base. Eligiendo además otro vector de base independiente de él, es decir, no generable por él (es decir aún, no compuesto de tonos, como sería 81/64, dos tonos), podremos representar ese espacio pitagórico. Por ejemplo, eligiendo la cuarta justa (4/3) como nuevo vector de base, encontramos en efecto:
@(-3,2) + 0@(2,-1) un tonosegunda 9/8 -- 1
tercera 81/64 -- 2
@(-3,2) + 0@(2,-1) dos tonoscuarta 4/3 -- 0
@(-3,2) + 1@(2,-1) una cuartaquinta 3/2 -- 1
@(-3,2) + 1@(2,-1) un tono y una cuartasexta 27/16 -- 2
@(-3,2) + 1@(2,-1) dos tonos y una cuartaséptima 243/128 -- 3
@(-3,2) + 1@(2,-1) tres tonos y una cuartaoctava 2/1 -- 1
@(-3,2) + 2@(2,-1) un tono y dos cuartascomo es evidente en el lenguaje musical. Si incluso elegimos el tono y semitono pitagóricos (9/8 y 256/243) como base llegaremos cómodamente a las definiciones habituales en solfeo del tipo 'una octava son 5 semitonos y 2 semitonos'; otra muestra de la adecuación de estos espacios al lenguaje habitual de la música.
Véase que el cambio de base sólo afecta a la 'posición' de las líneas quebradas que representan las escalas, pero no a su 'forma' y por lo tanto, no las distancias entre puntos: el cambio de base 'gira' las figuras pero no las 'deforma', no cambia las distancias.
Es muy fácil hallar las nuevas coordenadas de un intervalo o punto al cambiar de base, pero no entraremos en ello para no sobrecargar en exceso las herramientas matemáticas puestas en juego para ilustrar escalas y consonancia ( a la espera de que la enseñanza musical vuelva a incluir las matemáticas como una importante base de la formación de los alumnos).
Podemos decir que el espacio EP es un espacio musical, en el sentido de que plasma las relaciones musicales, las percibidas como tales.
TEORÍA DE LA CONSONANCIA ESENCIAL
Directamente basada en la de Euler, solamente la simplifica, adaptándola alos espacios EP recien definidos, y al tiempo, la generaliza.
Si un número natural A es expresado como producto de primos, define su grado de complejidad esencial como CE(A), como:
i i
A =
1 pi ai entonces: CE(A) = E ai@(pi-1)siendo pi (p sub i) los factores primos de A, ai (a sub i) sus exponentes, y
1 y E los signos de producto y sumatorio. Vemos que coincide con la medida de Euler, excepto que no adiciona 1:|
|
| i i | |||
| A = | A pi ai entonces | EC(A) = 1 + E ai@(pi-1) | (5) |
|
i i A = A pi ai entonces: EC(A) = 1 + E ai@(pi-1)
|
CE(A) = EC (A) -1 EC(A) = CE (A) + 1
Por ejemplo la complejidad de 8 (2 al cubo ) es 3.(2-1)=3 mientras que la de 9 es 2(3-1)=4, es decir 8 es más sencillo que 9.
El grado (de disonancia) de un intervalo reducido a números mínimos es simplemente el grado del producto de numerador y denominador. Así, la quinta 3/2 tiene el grado 3, el de 6 (2+1), la cuarta 4/3 tiene 4 (2+2), etc.
En general el grado de Disonancia Esencial de un conjunto de notas, como un acorde, vendra dado por la Complejidad Esencial del número cociente entre el mínimo común múltiplo y el máximo común divisor de sus frecuencias:
|
i i A = A pi ai entonces: EC(A) = 1 + E ai@(pi-1)
|
/ m.c.m (a,b,c,.) \
DE (a,b,c,..) = CE(N) N = (
)))))))))))) )\ m.c.d (a,b,c,.) /
Con más generalidad definimos, para diferentes exponentes:
|
i i A = A pi ai entonces: EC(A) = 1 + E ai@(pi-1)
|
i i
A =
1 pi ai entonces: CEp(A) = ( E ai@(pi-1)p)1/p
siendo p un exponente que pondera los primos diferentemente según su tamaño; y, como antes,
pi (p sub i) los factores primos de A, ai (a sub i) sus exponentes, y
1 y E los signos de producto y sumatorio. Y, como antes:
El grado de Disonancia p-Esencial de un conjunto de notas, como un acorde, vendra dado por la Complejidad Esencial del cociente entre el mínimo común múltiplo y el máximo común divisor de sus frecuencias:
| m.c.m (a,b,c,.) | |||
| DEp (a,b,c,..) = CEp ( |
|
) | (5) |
| m.c.d (a,b,c,.) |
Por ejemplo, las frecuencias 220-330-440, la-mi-la, tienen una disonancia como acorde igual al grado de disonancia del cociente (3×4×110)/110 = 12, que es 2×(2-1)+1×(3-1) = 4; y lo mismo los acordes do-sol-do o mi-si-mi. El acorde mayor en su forma fundamental, como do-mi-sol, reducido a cifras sencillas, tendrá siempre unas frecuencias proporcionales a 4-5-6, lo que nos lleva a una disonancia igual a la complejidad de 60, que es 8 [(2×(2-1)+1×(3-1)+1×(5-1)], mientras que el menor, la-do-mi, proporcional a 5/6-1-5/4, o sea, 10-12-15, tiene un grado como el de 60, otra vez 8: Se observa que ambos acordes resultan igualmente consonantes o disonantes, lo que coincide con la apreciación general.
Otras inversiones de un acorde pueden variar la disonancia: por ejemplo, el caso sol-do-mi, proporcional a 3/4-1-5/4, o 3-4-5, da 8, como antes (a partir de 60) pero mi-sol-do, 5/4-3/2-2, o 5-6-8, da 9 (el de 120, 3+2+4 = 9): es una inversión ligeramente más disonante que la forma fundamental.
INTERPRETACIÓN musical DEL NUMERO N
El número N, definido en el párrafo anterior como el cociente entre máximo común múltiplo y mínimo común divisor de las frecuencias de las notas oídas simultáneamente, tiene una interesante interpretación sonora y musical. Primeramente, se comprende que dividir por el m.c.d de las frecuencias, elimina la tesitura del acorde, reduciendola a una escala común: de esta manera se igualan acordes en octavas diferentes. por ejemplo: N sería igual para los acordes do3-mi-3-sol3, de frecuencias (apénd.1): 262-262.5/4-262.3/2, que do5-mi-5-sol5, (1047-1047.5/4-1047.3/2): en efecto, para ambos, N1 = (262.4.3.5)/(262)=3.4.5; y N2 = (1047.4.3.5)/(1047)=3.4.5; son iguales, la tesitura no influye en la disonancia esencial; así, toda tríada proporcional a 4-5-6 tiene igual N y por tanto igual DE.
LOS ESPACIOS MËTRICO ( EP, CEp )
La familia de Disonancias Esenciales que acabamos de definir proporciona una una familia paralela de distancias a los Espacios Primales que ya vimos: en efecto, miden un intervalo como distancia entre notas, y diferentemente que el tamaño del intervalo medido en semitonos, comas o cents, que se ve en el párrafo siguiente (Espacio Melódico).
En efecto, las DEp que acabamos de definir son también distancias en ese espacio, pues cumplen las condiciones de tal:
1. d(a,b) => 0 La distancia entre dos puntos cualesquiera es positiva o nula
2. d(a,a) = 0 Solo es nula cuando ambos puntos son el mismo.
3. d(a,b) <=d(a,c)+d(c,b) La distancia entre dos puntos es igual o menor que la suma de distancias de esos puntos a un tercero cualquiera.
Puede demostrarse que en efecto, nuestra familia de DEp cumplen las tres propiedades, lo que nos conforma una Familia de Espacios Métricos, para cada valor de p, sienfo 1 <p < infinito.
La más característica, la Propiedad Triangular, la cual establece que la distancia entre dos puntos es menor o igual ( caso de tres puntos alineados) que la suma de distancias de esos puntos a un tercero, puede intuirse en el espacio para p=2. Se trata de un plano cuando tenemos sólo dos primos, y la distancia es la distancia en línea recta habitual en nuestro mundo.
Disponemos así de verdaderos Mapas que nos representan Notas a distancias unas de otras similares a la lejanía numérica o Disonancia. Todo fenómeno relacionado con lo tonal, Escalas, Grados, Modos, Modulaciones, Harmonía, Enharmonía, Microtonía, etc. puede ser representado en estos espacios que acabamos de introducir.
EL ESPACIO MELÓDICO, EM
Hemos visto la forma logarítmica de los intervalos y su composición y descomposición en esta forma. Imaginando las frecuencias como puntos sobre una recta, podemos considerar estos intervalos como vectores que nos llevan una frecuencia a otra.
f1 f2 f3
)))))))))))+)))))))))>)))))))))))))))))>)))))))))
I1 I2
+
)))))))))))))))))))))))))))>I
Viendo que la suma existe (I, suma de I1 e I2, es otro intervalo), el intervalo opuesto ( -I1 es el descendente si I1 es ascendente), y el producto por números reales ( por ejemplo, 3,123.. veces I1), es taambién otro intervalo; se ve enseguida que el conjunto de estos intervalos expresados, en forma logarítmica (como cantidades de semitonos, comas o cents) es un espacio vectorial idéntico al de los números reales, conocido por R en la literatura matemática.
DISTANCIA MELÓDICA Y DISTANCIA HARMÓNICA
Dos notas cualesquiera están separadas por dos tipos de distancia: la Intervalica y la Harmónica. Si ascendemos por una escala mayor, la primera de ellas crece sin parar mientras que la segunda es grande pero decrece en la quinta y más aún en la octava. Podemos imaginar una espiral donde la distancia interválica transcurre sobre la curva: pero ésta, al curvarse, vuelve a pasar cerca del punto de partida: se trata de la distancia harmónica ( véase nuevamente la Espiral Harmónica).
Estos dos conceptos de distancia, y sus percepciones, juegan un papel importante en los de contrapunto y harmonía.
DISONANCIA DE UN TIMBRE HARMÓNICO
Los conceptos anteriores pueden ser generalizados a la tímbrica ( o retrotraídos a ella, si se la considera madre de la harmonía):
Como en un timbre harmónico todas las frecuencias son múltiplos de un fundamental, si sus frecuencias relativas son f, 2f, 3f...y sus intensidades son w1, w2, w3,.. etc podemos considerar ese timbre como un aglomerado (clusters) de notas elementales simultáneas proporcionales a 1,2,3,4,.... Su disonancia crecerá entonces con el orden y complejidad de los harmónicos que intervienen: yn timbre con los harmónicos 1,2,3,4,y 6 será sencillo, casi banal. En cambio si incluye 7, 11, 13, 19, será rasposo y raro, incluso desagradable.
Por eso se golpea la cuerda del piano en lugares determinados, que evitan harmónicos indeseados, como el 7, el 11, etc..
VISIÓN GEOMÉTRICA DE UNA PIEZA HARMÓNICA EN LOS ESPACIOS EM Y EP.
Los dos espacios donde evolucionan las voces son la recta o Espacio Melódico y el Espacio Primal (EP) o Espacio Harmónico.
Elegimos una base del este segundo espacio formada por los vectores Octava (vector primal (1,0,0)), Quinta (-1,1,0) y Tercera Mayor (-2,0,1); y representamos este espacio en el plano colocando el eje de quintas vertical, positivo hacia arriba, y el de terceras mayores horizontal, positivo a a la derecha. El tercer eje, de octavas lo imaginamos perpendicular al papel, positivo hacia el observador. Se obtienen así un conjunto de capas u hojas, cada una de las cuales está en relación de octava con las vecinas y en la que todos los nombres de las notas son los mismos. Este espacio primal es el subespacio EP3, ya que sólo el 2, el 3 y el 5 aparecen en sus relaciones. Con esta base lo llamaremos EPA3, Espacio Primal Harmónico de orden 3, o simplemente EPA.
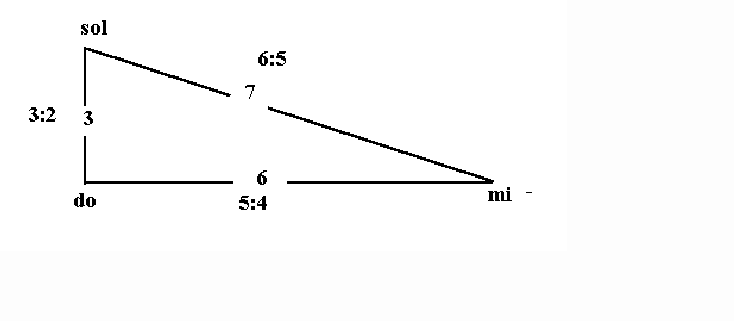 La ventaja de esta
representación reside en que los acordes mayor y menor quedan representados por
triángulos aproximadamente rectángulos; la DE de la quinta es 3, las de la
tercera mayor, 6 y la de la menor, 7, con lo que el ángulo 'recto' cae cerca de
la tónica ( en realidad es el exponente p=1.38 el que produce disonancias que
forman aángulo recto en nuestro mapa.):
La ventaja de esta
representación reside en que los acordes mayor y menor quedan representados por
triángulos aproximadamente rectángulos; la DE de la quinta es 3, las de la
tercera mayor, 6 y la de la menor, 7, con lo que el ángulo 'recto' cae cerca de
la tónica ( en realidad es el exponente p=1.38 el que produce disonancias que
forman aángulo recto en nuestro mapa.):
Toda poligonal es un acorde y su disonancia interna viene a ser la suma de los segmentos de la poligonal que les une. Se vuelve a observar la equivalente disonancia de los acordes mayor y menor.
Prolongando a derecha e izquierda terceras mayores ascendentes y descendentes sucesivas, y arriba y abajo, quintas ascendentes y descendentes, obtenemos un mapa donde cada nota y cada acorde queda situado respecto a los demás de acuerdo con su distancia harmónica ( y distancia perceptiva). Los parentescos quedan explicitados mediante contigüidades, las vecindades mediante proximidades. Resulta un verdadero mapa topológico (contigüidades) y Métrico (distancias) que visualiza la percepción, o así lo esperamos. He aquí el diagrama (pag.sigiente):
Todo acorde aparece a su vez en forma de poligonal tanto más extendida cuanto más diosnante es el acorde correspondiente. Las inversiones de los acordes no aparcen ya que se trata de cambios de octava, sólo repercuten en un salto de plano, lo que no aparece en la figura. Aparecen los acordes de séptima menor (de dominante) como como un signo de anzuelo _\, los de séptima mayor, como una z invertida, _\^, los de quinta aumentada como una L vista en el espejo, etc. Todo acorde tiene su forma y toda forma su acorde, de modo que se trata también de una especie de escritura o codificación.
Empleamos la notación de comas Hölder que hemos introducido en el apéndice.1; ahora bien, como que se trata también de una escala aproximada, la coincidencia de nombres que pueda observarse es también solo aproximada. En realidad, nunca se repite ninguna nota ni en vertical (quintas) ni en horizontal (terceras mayores) , ni en oblicuo (terceras menores) pues ya sabemos que es imposible conseguir una octava mediante quintas y terceras; o, en términos de espacio vectorial, conseguir un vector de base mediante los demás, por ser independientes. Lo que se consiguen son notas vecinas en el espacio melódico, tanto más cuanto más nos alejemos.
Simplificando aún más la notación, por ejemplo, en la temperada occidental obtenemos un esquema (pag. siguiente) aún más sencillo donde las repeticiones se consiguen antes: cada tres vértices en horizontal (tres terceras mayores, seis tonos temperados), cada 12 vértices en vertical (12 quintas), cada cuatro vértices en oblícuo a la derecha (cuatro terceras menores, 6 tonos), similar al movimento del alfil en ajedrez, cada 12 vértices en oblicuo a la izquierda (12 semitonos), el otro alfil, cada dos 'saltos de caballo ascendentes (cuarta aumentada) etc. Es decir todas las maneras de subdividir el número 12 (semitonos en la octava) .
¿Qué significado musical tienen estas repeticiones? Son las Enharmonías, que asímilan como vecinas tonalidades realmente muy lejanas, basándose en la cercanía melódica o interválica. Se aprecian aquí diferentes tipos de enharmonía, dependiendo de las direcciones o sentidos que hemos visto antes.
MAPAS TONALES
| a-a de vec5ndades t6na3es en 4n s5ste0a te0-erad6 y enhar0´6n5c6. |
ESQUEMA DE PARENTESCO entre NOTAS NO TEMPERADAS
RELACIONES con la TEORÍA de las REGIONES de SCHÖNBERG
Veamos ahora la relación y convergencia entre nuestro Espacio Primal y la Tradición Harmónica.
Aunque no indispensable para la validez musical de los conceptos anteriores, si resulta un respaldo (confortante e inmenso respaldo) la convergencia del esquema anterrior con las nociones usuales en la Harmonía Tradicional. Particulharmente es notable la casi coincidencia con uno de sus teóricos y prácticos más notables, Schönberg, quien, en sus dos libros [ ] y [ ], entre 1911 y 1945, realiza una especie de informe (¿final?) de este importante recurso expresivo. En el segundo de estos tratados presenta, para las tonalidades Mayor y Menor, unos esquemas de las tonalidades vecinas, que son una imagen especular del esquema anterior, el cual como sabemos ha sido rigurosamente deducido de la distancia en el Espacio Primal Ep.
Los esquemas de Schönberg y el nuestro son los siguientes:
|
|
||||||||||||||||||||||||||||||
| Esquemas harmónicos de Schönberg y nuestro Mapa Harmónico, comparados. | |||||||||||||||||||||||||||||||
Se observan laas mismas contigüidades o parentescos tonales en ambos esquemas, aunque a diferentes lados (izquierda en uno lo que es derecha en el otro: los mapas son pues similares. De este modo observamos otra de la notables coincidencias entre la Percepción y el Número: como ya hemos dicho, muestra una vez más que la Percepción musical es, en gran parte al menos, numérica.
LA CADENCIA
Sentimos la cadencia como una Afirmación y Resumen de la Tonalidad. Observemos ahora las cadencias bajo el prisma que nos proporcionan nuestras medidas de disonancia.
PRINCIPIOS BÁSICOS DE CONDUCCIÓN DE VOCES, REDEDUCIDOS.
PCV1. La harmonía cuenta la evolución en una obra cualquiera, del proceso consonancia -disonancia-consonancia. La primera Establece y Plantea, la segunda Crea y Presenta los problemas, la tercera los Resuelve.
Se percibe la semejanza con el proceso dramático Planteamiento-Nudo-Desenlace, el mismo proceso psicológico con medios expresivos diferentes.
PCV2. Cada voz evoluciona manteniendo dos tipos de relaciones consigo misma (notas precedentes y siguientes) y con las demás. La primera es su distancia melódica. La segunda su distancia harmònica.
PCV3. Dentro de cada voz, son aconsejables cambios melódicos más pequeños que su distancia a otras voces, si se quiere mantener la individualidad perceptiva de esa voz.
PCV4. Son aconsejables movimientos contrarios en las voces si se desea acentuar esa individualidad perceptiva de las voces: movimiento en igual sentido tienede a fundir varias voces en otra, más densa timbricamente..
(Viene a nuestra memoria la técnica de caza de los indios americanos para divisar un aanimal de caza en la pradera: mover la cabeza, para que el diferente ángulo con que se perciben objetos cercanos y lejanos, individualice, destaque al animal como figura sobre un fondo).
El caso más opuesto son las octavas y quintas paralelas, tradicionalmente 'prohibidas': su fusión en mayor, por tender a formar un lazo adicional: pertenencia a la misma serie harmónica.
PCV5. Una relación adicional de todas las voces es la doble relación melódica y harmónica con la tónica, si la hay. La habrá si fue sugerida con suficiente claridad al comienzo de la pieza.
PCV6. Todo cambio en una o más voces establece una nueva situación. Si el cambio harmónico es pequeño y el melódico grande se trsata de un 'cambio de posición', en sentido amplio. Si el cambio harmónico es grande y el melódico pequeño se trata de una resolución harmónica si disminuye la disonancia y una tensión si al revés.
PCV7. Una resolución harmónica sobre acordes cercanos a la referencia es una cadencia.
PCV8. Una resolución harmónica sobre acordes (más) lejanos a la referencia es una anticadencia.
PCV9. Se establece una referencia mediante una consonancia fuerte y duradera, al principio de la pieza.
DEFENSA DEL NÚMERO EN MÚSICA EN CONDICIONES ADVERSAS.
Resulta trabajoso defender una idea que nos parece evidente: la Música es Número Sonoro. Pero las tendencias musicales de las últimas décadas, dedicadas precisamente a disonver a abominar de esos números por causa del agotamiento estético que su aplicación ha producido, o por causa del agotamiento vital y espiritual del músico moderno, que como el personaje de la fábula, tira el niño junto al agua del baño, y busca tras romper su mejor juguete, otros más llamativos, exóticos, o simplemente interesantes o sorprendentes. Sea como fuere el número suena hoy a antigualla, a concepción abstracta alejada de lo musical, a especulación teórica, sea esto lo que sea, etc.
Contrariamente, a nosotros nos parece que sin ese número, reflejado en proporciones sencillas (= comprensibles en la percepción) entre cualidades-magnitudes del sonido, pricipalísimamente tono y duración, no cabe ya hablar de música, salvo por analogía. Y no es esto defender un principio, postura ética y metafísica perfectamente defendible; sino apelar a la propoia percepción, que siempre y en cualqioer parte reconocerá octava y quinta como intervalos notables usables, en música, o reconocera un ritmo basado en cuatro partes como simple, y el basado en diecisiete como complicado. Quien asegure que eésto es especulación teórica, que mida un compás de PI por 8 (3.141592 por 8), o cante con justeza una escala que progrese cada grado PI semitonos (314.1592 cents).
Todo ésto no es sólo Cultura, que también lo es; pero es sobre todo Naturaleza, que ha condicionado la Cultura, filtrando, suprimiendo aquellos intentos no del todo compatibles con ella. Poe ello, sólo por ello, se sigue haciendo música con octavas, quintas, cuartas ( más o menos retocadas por temperamentos y expresividades), y creando retornos rítmicos cada pocas unidades de un pulso regular (tempo).
Intentos más o menos drásticos han desarrollado el lenguaje musical, pero no han destruído, no pueden, estas bases tan sólidas de lo sonoro. La música llamada concreta, usando ruidos sin tono, ampliaba el repertorio de timbres y figuras rítmicas: pero trompas, falutas, pianos, siguen apareciendo en las orquestas. El serialismo dodecafónico incentiva lo sistemático en la motivación musical, y rompe la preponderancia de una nota sobre las demas (atonalidad): pero su funcionamiento depende de evitar cuidadosamente toda referencia tonal o harmónica tradicional. la aparición de un acorde de Fa mayor, daría al traste con todo el conjunto tan cuidadosamente programado: y no sólo, insistimos, porque la tradición nos llama: también y sobre todo, porque la sencillez perceptiva de un acorde mayor lo destaca naturalmente como referencia. Así vemos las vanguardias como rupturas de viejos trajes gastados para confeccionarse otros más amplios: pero todos usan una y otra vez la tela, su urdimbre y sus pliegues, su adaptación al cuerpo humano.
La complicación harmónica de una obra las millones de relaciones que se establecen, no deben hacernos olvidar la sencillez de donde proceden, como una catedral no hace olvidar la sencillez del sillar o el ladrillo: o la complejidad de la figura de un arbol procede de pocas reglas de division de ramas y ángulos entre ellas: un principio simple, indefinidamente repetido da lugar a complicaciones tremendas: el deseo de lucro produce el complicado juego del comercio, las finanzas, la bolsa, viajes, culturas.
BIBLOGRAFÍA
CHAILLEY, J. Traité historique d'analyse harmonique. Leduc. Paris.1976.
HABA, A. Nuevo Tratado de Harmonía R.musical Madrid,1979
HELMHOLTZ, H. On the Sensation of Tone. Dover N.York,1954
HERF, F. R(com). Mikrotöne I Helbling Innsbruck. 1985
HERF, F.R(com) Mikrotöne II Helbling Innsbrruck. 1987
HESSE, H.P. Grundlagen der Harmonik in mikrotaler MusiK . Helbling Innsbr. 1989
HINDEMITH, P. Harmonía Tradicional Ricordi B.Aire,1949
MESSIAEN, O. Technique de mon Langage musical Leduc Paris 1944
MICHACA VALENZUELA, P. La evolucion de la harmonía a través del principio cíclico-tonal. Univ. Nac. Autónoma. México.1972.
RIEMANN,H. Composición musical. Labor. Barcel.1950
SALZER,F. Structural Hearing.(2 vol). Dover, N.York,1962
SÁNCHEZ, F.J. (1977) "Application of Dissimilarity and Aperiodicity Functions to Pitch Extraction and Voiced-Unvoiced Decision in Speech" , Madrid,9. ICA Congress.
Sánchez, F.J.(1979) Tratamiento Señales Pseudoperiódicas. , Madrid, Ph.D. U.P.M.
Sánchez, F.J.(1989) "Interválica musical subyacente en la prosodia". Symp. Ling. Log, y Artes del Lenguaje., Madrid, Resid.Estudiantes, C.S.I.C.
Sánchez, F.J.& H.BERGÉ & E.GLADSTONE.(1995) Memoria Interna , Madrid, LTPM.
SÁNCHEZ, F.J. "Dissimilarity and Aperiodicity Functions. Temporal processing of Quasíperiodic Signals". 9º. ICA Cong., Madrid,1977.
SÁNCHEZ, F.J.: "Application of Dissimilarity and Aperiodicity Functions to Pitch Extraction and Voiced - Unvoiced Decision". 9.ICA Cong., Madrid,1977.
Sánchez, F.J. Tratamiento Señales Pseudoperiódicas. Ph. D. Un. Polit. Madrid,1979
Sánchez, F.J. La Música Culta Arabe Oriental Coop. Univ. Madrid, 1985
Sánchez, F.J "Analisis de interv.y escalas modales". Rev. Esp. Mus. Madrid,1989
Sánchez, F.J "The 8/7 interval in arab and related music". Mus. Sympos. Bagdad.1989
Sánchez, F.J . "Interválica musical subyacente en la prosodia". Sym. Ling. Log. Madrid.1989
Sánchez, F.J. Acústica musical II:Intervalos&Consonancia . U.A.M. Madrid,1989
Sánchez, F.J. Curso Acústica musical III: El Motivo. U.A.M. Madrid,1990
Sánchez, F.J "Number as Music Builder: Sonance". Symp.Mús.Inform.Delfos,1992
Sánchez, F.J. Acústica musical V: Ritmo, Motivo, Sonan. Comp. U.A.M.Madrid,1993
Sánchez, F.J. (Hesse,H. Ed) "Beyond 12-interval temperament in Arab Music". Musiked Nymphe Munchen, 1993
SCHENKER,H. Tratado de Harmonía. Real musical. Madrid, 1980.
SCHOENBERG,A. Tratado de Harmonía R.musical. Madrid,1979
SCHOENBERG,A. ¨Funciones Estructurales de la Harmonía. Labor. Barcelona,1990.
TOCH,E. La Melodía. Nacion. Mejico,1967
[ 1] BARKER,A.(ed) Greek musical Writings,II:Harm&Acous.Theory Univ.Pres.Cambridge.1989
[ 2] BENADE,A.H. Fundamentals of musical Acoustics. Oxford, N.York,1976
[ 3] BLACKWOOD,E. The Struct.of Recognizable Diatonic Scales Princ.Pr. Princeton.1985
[ 4] DomCARDINE. Semiología Gregoriana.Abadia de Silos, 198.
[ 5] CHERKI, S. Al-Moustadraf dans le regles.. Rabat, 1972
[ 6] DANIELOU,A. Traité de Musicologie Comparée. Hermann, Paris, 1959
[ 7] DURING,J. Le repertoire modele de la mus. iranienne: Radif. Soroush, Teheran,1991
[ 8] ERLANGER,R.D' La Musique Arabe. Vol.1-6 Geuthner, Paris 49-64
[ 9] GEVAERT,F.A. Histoire&Théorie d.l.Musique d.l'Antiquité G.Olms, Hildes 1965
[10] GUETTAT, M. La Musique Clasíque du Maghreb. Sindbad, Paris, 1980
[11] HAKKI,I,Ö. Türk Mûsikîsi Nazariyati ve Usûlleri. Ötüken Ne, Istanbul,1984
[12] HELMHOLTZ,H. On the Sensation of Tone. Dover, N.York,1954
[13] HERF,F.R(com) Mikrotöne I,II Helbling , Innsbruck.1985,1987
[14] JARGY,Simon La Musique Arabe (Que sais je?) P.U.F., Paris, 1971
[15] JEANNETEAU,J. Los Modos Gregorianos Abadía de Silos, 1985
[16] Al-KATIB Kitab Kamal Adab Al-Gina Siria,s.IX
(SHILOAH,A.) La Perfection des Conn.Music. Geuthner, Paris, 1972
[17] Al-Fasí Kitab Al Jumu Fi Al Musiqi ...
(FHARMER,H.G.) An Old Moorish Lute Tutor Civil Pr. Glasgo,1933
[18] Coll.Int.du C.N.R.S Acoustique musicale(Marseille,1958) C.N.R.S, Paris 1959
[19] KASZIM, A Terminology of Oriental Music AlJamhuri, Bagdad,1964
[20] KARAS,S. Harmonika:Des consonances par moyens harmoniques. Manoutios. Athène.1989
[21] KARADENIZ, E. Turk Mûsikîsinin Nazariye... T.Bank.Y Ankara,1965
[22] LACHMANN,R. Música de Oriente. Labor, Barcel.1931
[23] LEON TELLO,F. Estudios de Historia de la Teoría musical. C.S.I.C. Madrid.1962
[24] LLOYD,H.B Intervals, Scales and Temperament. S.Martin N.York,1963
[25] MALM, W.P. Culturas Mus.Pacifico,Cercano Oriente&asía Alianza, Madrid,1985
[26] MAHDI,Sal.El La Musique Arabe. Leduc, Paris, 1972
[27] ÖZCAN, I.H. Türk Mûsikîsi Nazariyati ve Usulleri. Ötüken, Istamb.1984
[28] ROEDERER,J.G. Intr.Physics and Psychoacoustics of Music. Springer, N.York,1979
[29] Al-RAJAB,H Al Maqam Al-Iraqui. Al-Ma'arif, Bagdad,1961
[30] REINHART,K&U. Turquie. Les Traditions musicales. Buchet/Ch.Paris, 1969
[31] SACHS,K. La Música en la Antiguedad. Labor. Barcelona.1934
[32] SACHS,K. Musicología Comparada. Eudeba, B.Aires,1966
[46] STRANGEWAYS.F The Music of Hindostan Orie.Rep. Delhi 1975
[47] TOBIAS,J.V. Foundations of Modern Auditory Theory Ac.Pres N.York,1970
[48] TOUMA,H.H. La Musique Arabe Buch/Chat.Paris, 1977
[49] WINCKEL,F. Music, Sound and Sensation Dover, N.York 1967
[50] YEKTA BEY,R. Türk Mûsikîsi Nazariyati ve Usûlleri. Pan Y. Istanbul,1986
BACKUS, The Acoustic Foundation of Music Norton N.York,1977
BENADE,A.H. Fundamentals of musical Acoustics. Oxford N.York,1976
BLACKWOOD,E. The Struct.of Recognizable Diatonic Scales Princ.Pr. Prince.1985
BUASSE,H. Instruments a Vent Delagrave Paris, 1929
CULVER,C.A. musical Acoustics McGraw H. N.York,1956
DANIELOU,A. Traité de Musicologie Comparée. Hermann Paris, 1959
ERICKSON,R. Sound Structure in Music Calif.Pr. Berkel.1975
ERLANGER,R.D' La Musique Arabe. Vol.1-6 Geuthner Paris 49-64
KENT,E.L. musical Acoustics Dowden Stroud.1877
LACHMANN,R. Música de Oriente. Labor Barcel.1931
LEIPP,E. Acoustique et Musique Masson Paris, 1976
LLOYD,H.B Intervals, Scales and Temperament S.Martin N.York,1963
MERCIER.J. Traité d'Acoustique Press Uni Paris 1962
OLSON,H.F. Music, Physics and Engineering. Dover N.York,1967
ÖZCAN, I.H. Türk Mûsikîsi Nazariyati ve Usulleri Ötüken Istamb.1984
PIERCE,J.R. Los Sonidos de la Música Sci.Ameri.Barcel.1985
RANDALL,H.R. An Introduction to Acoustics Addison Camb.M.1951
ROEDERER,J.G. Intr.Physics and Psychoacoustics of Music Springer N.York,1979
SACHS,K. Musicología Comparada Eudeba B.Aires1966
STRANGEWAYS.F The Music of Hindostan Orie.Rep. Delhi 1975
TOBIAS,J.V. Foundations of Modern Auditory Theory Ac.Pres N.York,1970
WINCKEL,F. Vues Nouvelles sur le Monde des Sons. Dunod, Paris, 1960
WINCKEL,F. Music, Sound and Sensation . Dover, N.York 1967
WOOD,A.B. A Text-book of Sound. Bell&Sons London,1944
Varios. Les Instruments de l'Orchestre Sci.Ameri.Paris, 1985
APÉNDICES.
1. AFINACIONES y NOTACIONES BASADAS EN DIVISIONES IGUALES DE LA OCTAVA.
SEMITONO TEMPERADO
Este sistema musical, vigente ahora en todo el mundo, toma una nota (frecuencia) de referencia y construye a partir de ella dos sucesiones de frecuencias tales que su razón es el semitono temperado ( 1.059, 6%) y su diferencia en cents, 100, por definición. Aparecen pues 12 notas por octava, extendíendose la tesitura total en un rango desde unos 33 hercios hasta unos 8000; este límite lo fija la percepción de tono; por encima de esta frecuencia se percibe solo un silbido (algunos instrumentos se extienden aún más, no obstante).
Obtenemos así un rango útil de tonos de unas 8 octavas.
33- 65 - 130 - 261-520-1040-2080-4160-8320-
1 2 3 4 5 6 7 8
El sistema de notación es tradicional y utiliza los conocidos símbolos siguientes:
do re mi fa sol la si
c d e f g a b
en los países de influencia latina (arriba) y los de influencia anglosajona (abajo). Se nota que los primeros comienzan por una referencia do, que corresponde al tercero de los segundos, los cuales comienzan por a ( el sexto de los primeros).
¿A qué frecuencias corresponden estos nombres?. Esto ha cambiado a lo largo de la historia, generalmente subiendo poco a poco la frecuencia (más de un tono, 204 cents, en varios siglos).
Actualmente se adopta, al menos de palabra, la referencia la=440hz. lo que no obsta para que instrumentos modernos se afinen más y más altos. Tras comparar los sistemas francés, americano y de piano, elegimos el que consideramos más generalizado en nuestro ambiente, asignando 440 hz. a la octava 3; de modo que :
Diapason: LA 3 = 440 hercios.
las demás notas quedan inmediatamente fijadas por ese La 3. Admitiendo los valores teóricos de los intervalos, obtenemos el cuadro adjunto.
En realidad estos valores son solo aproximados: en efecto, el oido precisa intervalos mayores que los teóricos para la sensación correspondiente. Podemos pues añadir unos 5 cents por octava en las centrales y bastante más en las extremas. De modo que la separación real entre dos notas separadas por 6 o 7 octavas es al menos 100 cents mayor que la teórica (piénsese la importancia de este hecho, generalmente ignorado por los afinadores, constructores y usuarios de sintetizadores electrónicos).
COMA HÖLDER
Para representar con más precisión los matices de afinación de escalas tradicionales, no cubiertos por la nomenclatura anterior, es necesario disponer de divisiones más finas. La notación que adoptamos es la basada en la división de la octava en 53 partes iguales, iguales a la coma Hölder, como es sabido: con un error menor un par de cents quedan aproximadamente reflejados los intervalos de las escalas habituales: las mayores pitagórica y temperadas aparecen sin alteraciones, la natural de Zarlino con la tercera, sexta y séptima una coma bajas (-),etc. La escala de referencia es, con un ligero error (1.5 cent, max) la escala pitagórica o de quintas (véase esta escala en el el tema 3).
Las desviaciones con respecto esta escala de base se expresan mediante el número de comas que se suben o bajan, segun la lista que sigue:
comas sube baja
1 + -
2 ++ =
5 b
Así cubriremos todas las notas; por ejemplo en los tonos:
notas: do do+ do++ reb- reb reb+ reb++ re= re- re
comas: 1 2 3 4 5 6 7 8 9
y en
los semitonos:notas: mi mi+ fa= fa- fa
comas: 1 2 3 4
quedando similharmente representadas las demás. Esta notación es similar, pero no idéntica a la usada por Danielou [10], y, por otra parte, la música turca tradicional [17],[30]. La notación del primero, muy precisa, resulta algo enrrevesada, al utilizar una escala de base de Zarlino, con tonos mayores y menores, bemoles de cuatro comas e intervalo 1/4 extraño al concepto de coma. La segunda emplea como base la escala pitagórica o de quintas, pero emplea hasta 8 tipos de sostenido y bemol, para configurar las escalas de los modos turcos. Estas notaciones aparecen en el tema 6.
Hemos preferido nuestra notación por encontrarla a la vez más sencilla e intuitiva. En la medida de la calidad de un temperamento, tema 3, se muestra la asombrosa precisión de esta división para dar cuenta de las escalas tradicionales.
ESPACIO VECTORIAL
La idea de vector es la de 'cantidad con dirección', como la fuerza mayor o menor (cantidad) que se ejerce con una orientación (empujamos hacia o contra algo). En definitiva, precisamos más de un número para determinar o conocer un vector). Otra idea importante es la de que los vectores pueden componerse o sumarse: pero en esta suma vectorial, la efectividad de la suma depende de las orientaciones y magnitudes de los sumandos: dos fuerzas iguales y opuestas se anulan mutuamente, su 'suma' es nula.
Los vectores pueden pues sumarse o componerse, y también descomponerse, es decir, encontar vectores cuya suma sea el dado, al igual que podemos decir que '5 puede obtenerse como suma de 2 y 3, o bién, de 1 y 4'. Para un vector diríamos entonces que esos vectores son sus componentes.
El espacio vectorial es pues un conjunto de elementos que pueden sumarse entre sí dando lugar a elementos del propio conjunto; incluso dado el concepto de producto como suma simplificada ( 2a=a+a), también el producto de un número por un vector será también otro vector del conjunto (cuidado que no hablamos de producto de vectores). Pensemos en fuerza doble, o triple. Además en este tipo de espacios, debe existir además un vector que sumado a otro no le modifique, un elemento neutro o trivial, el vector nulo.
Todo este preámbulo describe las condiciones para que un conjunto sea un espacio vectorial, condiciones que sumarizamos en la definición siguiente:
Un conjunto es un Espacio Vectorial cuando:
1. La suma de dos elementos culesquiera del conjunto es tambiénelemento del conjunto. (suma conmut.,trans.,distributiva)
2. El producto de cualquier elemento del conjunto por un número real es también un elemento del conjunto.(dist,con,1)
3. Hay en el conjunto un elemento que sumado con cualquiera otro resulta el mismo (no le modifica).
4. Hay en el conjunto por cada elemento, otro llamado su opuesto, el cual sumado con el resulta el neutro.
En lenguaje matemático convencional, con una aplicación simultánea al conjunto de los Enteros:
V es un espacio vectorial cuando cumple:
, V El suma de dos enteros es otro entero; 8 + (-5) = 3V1. a + b
V2.
a"b , V El producto de un entero por otro es otro entero: 5 por -3 es -15.V3. a +
1 = a Hay un vector neutro, el 0: sumado a cualquier entero, éste no varía; 0 + 5 =5V4. a + (-a) =
1 Hay un vector opuesto para cada entero: para 3, -3 (3+(-3)=0Estas operaciones cumplen algunas otras propiedades, las normales (conmutativa, distributiva, asociativa, etc)
En música, como en cualquier otra disciplina, encontramos multitud de espacios vectoriales: los intervalos como tamaño, que veremos en otro momento ( Espacio Melódico ) son un caso particulharmente interesante; pero también el los intervalos como n-uplas en el espacio de primos que acabamos de ver, que ampliaremos posteriormente.
Vuelta al Principio